| Date | May 2008 | Marks available | 3 | Reference code | 08M.1.sl.TZ1.8 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
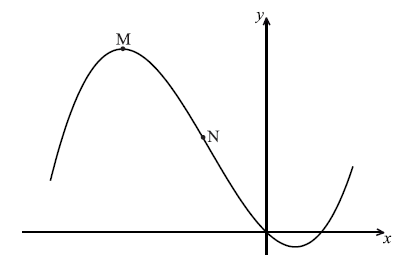
Consider \(f(x) = \frac{1}{3}{x^3} + 2{x^2} - 5x\) . Part of the graph of f is shown below. There is a maximum point at M, and a point of inflexion at N.
Find \(f'(x)\) .
Find the x-coordinate of M.
Find the x-coordinate of N.
The line L is the tangent to the curve of f at \((3{\text{, }}12)\). Find the equation of L in the form \(y = ax + b\) .
Markscheme
\(f'(x) = {x^2} + 4x - 5\) A1A1A1 N3
[3 marks]
evidence of attempting to solve \(f'(x) = 0\) (M1)
evidence of correct working A1
e.g. \((x + 5)(x - 1)\) , \(\frac{{ - 4 \pm \sqrt {16 + 20} }}{2}\) , sketch
\(x = - 5\), \(x = 1\) (A1)
so \(x = - 5\) A1 N2
[4 marks]
METHOD 1
\(f''(x) = 2x + 4\) (may be seen later) A1
evidence of setting second derivative = 0 (M1)
e.g. \(2x + 4 = 0\)
\(x = - 2\) A1 N2
METHOD 2
evidence of use of symmetry (M1)
e.g. midpoint of max/min, reference to shape of cubic
correct calculation A1
e.g. \(\frac{{ - 5 + 1}}{2}\)
\(x = - 2\) A1 N2
[3 marks]
attempting to find the value of the derivative when \(x = 3\) (M1)
\(f'(3) = 16\) A1
valid approach to finding the equation of a line M1
e.g. \(y - 12 = 16(x - 3)\) , \(12 = 16 \times 3 + b\)
\(y = 16x - 36\) A1 N2
[4 marks]
Examiners report
This question was very well done with most candidates showing their work in an orderly manner. There were a number of candidates, however, who were a bit sloppy in indicating when a function was being equated to zero and they “solved” an expression rather than an equation.
This question was very well done with most candidates showing their work in an orderly manner. There were a number of candidates, however, who were a bit sloppy in indicating when a function was being equated to zero and they “solved” an expression rather than an equation. Many candidates went through first and second derivative tests to verify that the point they found was a maximum or an inflexion point; this was unnecessary since the graph was given. Many also found the y-coordinate which was unnecessary and used up valuable time on the exam.
This question was very well done with most candidates showing their work in an orderly manner. There were a number of candidates, however, who were a bit sloppy in indicating when a function was being equated to zero and they “solved” an expression rather than an equation. Many candidates went through first and second derivative tests to verify that the point they found was a maximum or an inflexion point; this was unnecessary since the graph was given. Many also found the y-coordinate which was unnecessary and used up valuable time on the exam.
This question was very well done with most candidates showing their work in an orderly manner. There were a number of candidates, however, who were a bit sloppy in indicating when a function was being equated to zero and they “solved” an expression rather than an equation. Many candidates went through first and second derivative tests to verify that the point they found was a maximum or an inflexion point; this was unnecessary since the graph was given. Many also found the y-coordinate which was unnecessary and used up valuable time on the exam.

