| Date | May 2011 | Marks available | 5 | Reference code | 11M.2.sl.TZ1.9 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Show that and Find | Question number | 9 | Adapted from | N/A |
Question
The following diagram shows the graph of \(f(x) = {{\rm{e}}^{ - {x^2}}}\) .
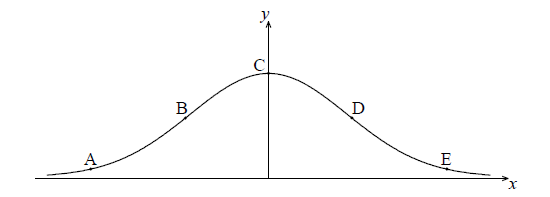
The points A, B, C, D and E lie on the graph of f . Two of these are points of inflexion.
Identify the two points of inflexion.
(i) Find \(f'(x)\) .
(ii) Show that \(f''(x) = (4{x^2} - 2){{\rm{e}}^{ - {x^2}}}\) .
Find the x-coordinate of each point of inflexion.
Use the second derivative to show that one of these points is a point of inflexion.
Markscheme
B, D A1A1 N2
[2 marks]
(i) \(f'(x) = - 2x{{\rm{e}}^{ - {x^2}}}\) A1A1 N2
Note: Award A1 for \({{\rm{e}}^{ - {x^2}}}\) and A1 for \( - 2x\) .
(ii) finding the derivative of \( - 2x\) , i.e. \( - 2\) (A1)
evidence of choosing the product rule (M1)
e.g. \( - 2{{\rm{e}}^{ - {x^2}}}\) \( - 2x \times - 2x{{\rm{e}}^{ - {x^2}}}\)
\( - 2{{\rm{e}}^{ - {x^2}}} + 4{x^2}{{\rm{e}}^{ - {x^2}}}\) A1
\(f''(x) = (4{x^2} - 2){{\rm{e}}^{ - {x^2}}}\) AG N0
[5 marks]
valid reasoning R1
e.g. \(f''(x) = 0\)
attempting to solve the equation (M1)
e.g. \((4{x^2} - 2) = 0\) , sketch of \(f''(x)\)
\(p = 0.707\) \(\left( { = \frac{1}{{\sqrt 2 }}} \right)\) , \(q = - 0.707\) \(\left( { = - \frac{1}{{\sqrt 2 }}} \right)\) A1A1 N3
[4 marks]
evidence of using second derivative to test values on either side of POI M1
e.g. finding values, reference to graph of \(f''\) , sign table
correct working A1A1
e.g. finding any two correct values either side of POI,
checking sign of \(f''\) on either side of POI
reference to sign change of \(f''(x)\) R1 N0
[4 marks]
Examiners report
Most candidates were able to recognize the points of inflexion in part (a).
Most candidates were able to recognize the points of inflexion in part (a) and had little difficulty with the first and second derivatives in part (b). A few did not recognize the application of the product rule in part (b).
Obtaining the x-coordinates of the inflexion points in (c) usually did not cause many problems.
Only the better-prepared candidates understood how to set up a second derivative test in part (d). Many of those did not show, or clearly indicate, the values of x used to test for a point of inflexion, but merely gave an indication of the sign. Some candidates simply resorted to showing that \(f''\left( { \pm \frac{1}{{\sqrt 2 }}} \right) = 0\) , completely missing the point of the question. The necessary condition for a point of inflexion, i.e. \(f''(x) = 0\) and the change of sign for \(f''(x)\) , seemed not to be known by the vast majority of candidates.

