| Date | May 2010 | Marks available | 2 | Reference code | 10M.1.sl.TZ1.9 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Explain | Question number | 9 | Adapted from | N/A |
Question
Let \(f(x) = \frac{{\cos x}}{{\sin x}}\) , for \(\sin x \ne 0\) .
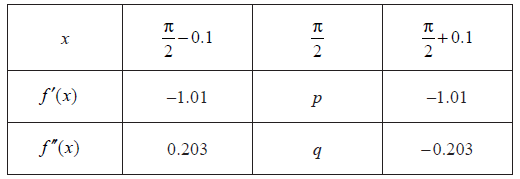
In the following table, \(f'\left( {\frac{\pi }{2}} \right) = p\) and \(f''\left( {\frac{\pi }{2}} \right) = q\) . The table also gives approximate values of \(f'(x)\) and \(f''(x)\) near \(x = \frac{\pi }{2}\) .
Use the quotient rule to show that \(f'(x) = \frac{{ - 1}}{{{{\sin }^2}x}}\) .
Find \(f''(x)\) .
Find the value of p and of q.
Use information from the table to explain why there is a point of inflexion on the graph of f where \(x = \frac{\pi }{2}\) .
Markscheme
\(\frac{{\rm{d}}}{{{\rm{d}}x}}\sin x = \cos x\) , \(\frac{{\rm{d}}}{{{\rm{d}}x}}\cos x = - \sin x\) (seen anywhere) (A1)(A1)
evidence of using the quotient rule M1
correct substitution A1
e.g. \(\frac{{\sin x( - \sin x) - \cos x(\cos x)}}{{{{\sin }^2}x}}\) , \(\frac{{ - {{\sin }^2}x - {{\cos }^2}x}}{{{{\sin }^2}x}}\)
\(f'(x) = \frac{{ - ({{\sin }^2}x + {{\cos }^2}x)}}{{{{\sin }^2}x}}\) A1
\(f'(x) = \frac{{ - 1}}{{{{\sin }^2}x}}\) AG N0
[5 marks]
METHOD 1
appropriate approach (M1)
e.g. \(f'(x) = - {(\sin x)^{ - 2}}\)
\(f''(x) = 2({\sin ^{ - 3}}x)(\cos x)\) \(\left( { = \frac{{2\cos x}}{{{{\sin }^3}x}}} \right)\) A1A1 N3
Note: Award A1 for \(2{\sin ^{ - 3}}x\) , A1 for \(\cos x\) .
METHOD 2
derivative of \({\sin ^2}x = 2\sin x\cos x\) (seen anywhere) A1
evidence of choosing quotient rule (M1)
e.g. \(u = - 1\) , \(v = {\sin ^2}x\) , \(f'' = \frac{{{{\sin }^2}x \times 0 - ( - 1)2\sin x\cos x}}{{{{({{\sin }^2}x)}^2}}}\)
\(f''(x) = \frac{{2\sin x\cos x}}{{{{({{\sin }^2}x)}^2}}}\) \(\left( { = \frac{{2\cos x}}{{{{\sin }^3}x}}} \right)\) A1 N3
[3 marks]
evidence of substituting \(\frac{\pi }{2}\) M1
e.g. \(\frac{{ - 1}}{{{{\sin }^2}\frac{\pi }{2}}}\) , \(\frac{{2\cos \frac{\pi }{2}}}{{{{\sin }^3}\frac{\pi }{2}}}\)
\(p = - 1\) , \(q = 0\) A1A1 N1N1
[3 marks]
second derivative is zero, second derivative changes sign R1R1 N2
[2 marks]
Examiners report
Many candidates comfortably applied the quotient rule, although some did not completely show that the Pythagorean identity achieves the numerator of the answer given. Whether changing to \( - {(\sin x)^{ - 2}}\) , or applying the quotient rule a second time, most candidates neglected the chain rule in finding the second derivative.
Whether changing to \( - {(\sin x)^{ - 2}}\) , or applying the quotient rule a second time, most candidates neglected the chain rule in finding the second derivative.
Those who knew the trigonometric ratios at \(\frac{\pi }{2}\)typically found the values of p and of q, sometimes in follow-through from an incorrect \(f''(x)\) .
Few candidates gave two reasons from the table that supported the existence of a point of inflexion. Most stated that the second derivative is zero and neglected to consider the sign change to the left and right of q. Some discussed a change of concavity, but without supporting this statement by referencing the change of sign in \(f''(x)\) , so no marks were earned.

