| Date | May 2013 | Marks available | 5 | Reference code | 13M.1.sl.TZ1.10 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Hence, Show that, and Find | Question number | 10 | Adapted from | N/A |
Question
Consider \(f(x) = \ln ({x^4} + 1)\) .
The second derivative is given by \(f''(x) = \frac{{4{x^2}(3 - {x^4})}}{{{{({x^4} + 1)}^2}}}\) .
The equation \(f''(x) = 0\) has only three solutions, when \(x = 0\) , \( \pm \sqrt[4]{3}\) \(( \pm 1.316 \ldots )\) .
Find the value of \(f(0)\) .
Find the set of values of \(x\) for which \(f\) is increasing.
(i) Find \(f''(1)\) .
(ii) Hence, show that there is no point of inflexion on the graph of \(f\) at \(x = 0\) .
There is a point of inflexion on the graph of \(f\) at \(x = \sqrt[4]{3}\) \((x = 1.316 \ldots )\) .
Sketch the graph of \(f\) , for \(x \ge 0\) .
Markscheme
substitute \(0\) into \(f\) (M1)
eg \(\ln (0 + 1)\) , \(\ln 1\)
\(f(0) = 0\) A1 N2
[2 marks]
\(f'(x) = \frac{1}{{{x^4} + 1}} \times 4{x^3}\) (seen anywhere) A1A1
Note: Award A1 for \(\frac{1}{{{x^4} + 1}}\) and A1 for \(4{x^3}\) .
recognizing \(f\) increasing where \(f'(x) > 0\) (seen anywhere) R1
eg \(f'(x) > 0\) , diagram of signs
attempt to solve \(f'(x) > 0\) (M1)
eg \(4{x^3} = 0\) , \({x^3} > 0\)
\(f\) increasing for \(x > 0\) (accept \(x \ge 0\) ) A1 N1
[5 marks]
(i) substituting \(x = 1\) into \(f''\) (A1)
eg \(\frac{{4(3 - 1)}}{{{{(1 + 1)}^2}}}\) , \(\frac{{4 \times 2}}{4}\)
\(f''(1) = 2\) A1 N2
(ii) valid interpretation of point of inflexion (seen anywhere) R1
eg no change of sign in \(f''(x)\) , no change in concavity,
\(f'\) increasing both sides of zero
attempt to find \(f''(x)\) for \(x < 0\) (M1)
eg \(f''( - 1)\) , \(\frac{{4{{( - 1)}^2}(3 - {{( - 1)}^4})}}{{{{({{( - 1)}^4} + 1)}^2}}}\) , diagram of signs
correct working leading to positive value A1
eg \(f''( - 1) = 2\) , discussing signs of numerator and denominator
there is no point of inflexion at \(x = 0\) AG N0
[5 marks]
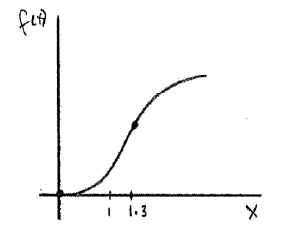 A1A1A1 N3
A1A1A1 N3
Notes: Award A1 for shape concave up left of POI and concave down right of POI.
Only if this A1 is awarded, then award the following:
A1 for curve through (\(0\), \(0\)) , A1 for increasing throughout.
Sketch need not be drawn to scale. Only essential features need to be clear.
[3 marks]
Examiners report
Many candidates left their answer to part (a) as \(\ln 1\). While this shows an understanding for substituting a value into a function, it leaves an unfinished answer that should be expressed as an integer.
Candidates who attempted to consider where \(f\) is increasing generally understood the derivative is needed. However, a number of candidates did not apply the chain rule, which commonly led to answers such as “increasing for all \(x\)”. Many set their derivative equal to zero, while neglecting to indicate in their working that \(f'(x) > 0\) for an increasing function. Some created a diagram of signs, which provides appropriate evidence as long as it is clear that the signs represent \(f’\).
Finding \(f''(1)\) proved no challenge, however, using this value to show that no point of inflexion exists proved elusive for many. Some candidates recognized the signs must not change in the second derivative. Few candidates presented evidence in the form of a calculation, which follows from the “hence” command of the question. In this case, a sign diagram without numerical evidence was not sufficient.
Few candidates created a correct graph from the information given or found in the question. This included the point (\(0\), \(0\)), the fact that the function is always increasing for \(x > 0\) , the concavity at \(x = 1\) and the change in concavity at the given point of inflexion. Many incorrect attempts showed a graph concave down to the right of \(x = 0\) , changing to concave up.

