| Date | November 2014 | Marks available | 4 | Reference code | 14N.1.sl.TZ0.3 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows a board which is divided into three regions \(A\), \(B\) and \(C\).
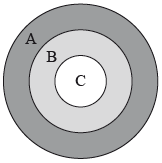
A game consists of a contestant throwing one dart at the board. The probability of hitting each region is given in the following table.
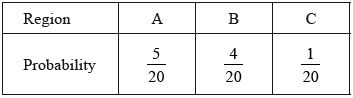
Find the probability that the dart does not hit the board.
The contestant scores points as shown in the following table.

Given that the game is fair, find the value of \(q\).
Markscheme
evidence of summing probabilities to \(1\) (M1)
eg\(\;\;\;\frac{5}{{20}} + \frac{4}{{20}} + \frac{1}{{20}} + p = 1,\;\;\;\sum { = 1} \)
correct working (A1)
eg\(\;\;\;p = 1 - \frac{{10}}{{20}}\)
\(p = \frac{{10}}{{20}}\;\;\;\left( { = \frac{1}{2}} \right)\) A1 N2
[3 marks]
correct substitution into \({\text{E}}(X)\) (A1)
eg\(\;\;\;\frac{4}{{20}}(q) + \frac{1}{{20}}(10) + \frac{{10}}{{20}}( - 3)\)
valid reasoning for fair game (seen anywhere, including equation) (M1)
eg\(\;\;\;{\text{E}}(X) = 0\), points lost\( = \)points gained
correct working (A1)
eg\(\;\;\;4q + 10 - 30 = 0,\;\;\;\frac{4}{{20}}q + \frac{{10}}{{20}} = \frac{{30}}{{20}}\)
\(q = 5\) A1 N2
[4 marks]
Total [7 marks]
Examiners report
The large majority of candidates answered part (a) of the question correctly by summing the probabilities to 1.
Part (b), however was not as well done. Many candidates seemed to be unfamiliar with the idea of a "fair game", despite this topic being listed in the syllabus. The most common error in part (b) was setting \(E(X) = 1\) rather than \(E(X) = 0\).

