| Date | November 2010 | Marks available | 8 | Reference code | 10N.2.sl.TZ0.9 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find and Show that | Question number | 9 | Adapted from | N/A |
Question
A test has five questions. To pass the test, at least three of the questions must be answered correctly.
The probability that Mark answers a question correctly is \(\frac{1}{5}\) . Let X be the number of questions that Mark answers correctly.
Bill also takes the test. Let Y be the number of questions that Bill answers correctly.
The following table is the probability distribution for Y .
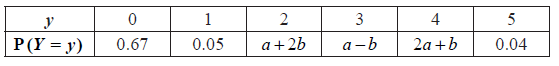
(i) Find E(X ) .
(ii) Find the probability that Mark passes the test.
(i) Show that \(4a + 2b = 0.24\) .
(ii) Given that \({\rm{E}}(Y) = 1\) , find a and b .
Find which student is more likely to pass the test.
Markscheme
(i) valid approach (M1)
e.g. \(np\) , \(5 \times \frac{1}{5}\)
\({\rm{E}}(X) = 1\) A1 N2
(ii) evidence of appropriate approach involving binomial (M1)
e.g. \(X \sim B\left( {5,\frac{1}{5}} \right)\)
recognizing that Mark needs to answer 3 or more questions correctly (A1)
e.g. \({\rm{P}}(X \ge 3)\)
valid approach M1
e.g. \(1 - {\rm{P}}(X \le 2)\) , \({\rm{P}}(X = 3) + {\rm{P}}(X = 4) + {\rm{P}}(X = 5)\)
\({\text{P(pass)}} = 0.0579\) A1 N3
[6 marks]
(i) evidence of summing probabilities to 1 (M1)
e.g. \(0.67 + 0.05 + (a + 2b) + \ldots + 0.04 = 1\)
some simplification that clearly leads to required answer
e.g. \(0.76 + 4a + 2b = 1\) A1
\(4a + 2b = 0.24\) AG N0
(ii) correct substitution into the formula for expected value (A1)
e.g. \(0(0.67) + 1(0.05) + \ldots + 5(0.04)\)
some simplification (A1)
e.g. \(0.05 + 2a + 4b + \ldots + 5(0.04) = 1\)
correct equation A1
e.g. \(13a + 5b = 0.75\)
evidence of solving (M1)
\(a = 0.05\) , \(b = 0.02\) A1A1 N4
[8 marks]
attempt to find probability Bill passes (M1)
e.g. \({\rm{P}}(Y \ge 3)\)
correct value 0.19 A1
Bill (is more likely to pass) A1 N0
[3 marks]
Examiners report
There was wide spectrum of success on this problem. Candidates could normally find E(X) using \(n \times p\) but many failed to recognize that the "experiment" was binomial or that for Mark to the pass the test, he needed to answer either 3, 4 or 5 questions correctly.
Part (b) was generally well done although there were a number of algebraic errors particularly in part (b) (ii), leading to incorrect values of a and b. Again, appropriate use of the GDC here would have eliminated these errors.
In (c), candidates had trouble with the command term, "find" and often just wrote down either "Mark" or "Bill".

