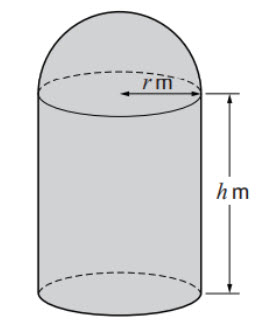
A container is made from a cylinder and a hemisphere. The radius of the cylinder is r m and the height is h. The volume of the container is \(45\pi\)
a) The volume of a hemisphere = \(\frac{2}{3}\pi r^3\)
The volume of the cylinder = \(\pi r^2h\)
Hence, the volume of the container = \(\frac{2}{3}\pi r^3+\pi r^2h\)
\(\frac{2}{3}\pi r^3+\pi r^2h=45\pi\)
We can divide through by \(\pi\) and rearrange to make h the subject of the formula
\(\frac{2}{3} r^3+ r^2h=45\)
\(r^2h=45-\frac{2}{3} r^3\)
\(h=\frac{45}{r^2}-\frac{2}{3} r\)
b) The surface area of the container = \(2\pi r^2+\pi r^2+2\pi rh\)
\(A=3\pi r^2+2\pi rh\)
\(A=3\pi r^2+2\pi r(\frac{45}{r^2}-\frac{2}{3} r)\)
\(A=\frac{9\pi r^2}{3}-\frac{4 \pi r^2}{3}+\frac{90 \pi}{r}\)
\(A=\frac{5\pi r^2}{3}+\frac{90 \pi}{r}\)
c) \(\frac{dA}{dr}=\frac{10\pi r}{3}-\frac{90 \pi}{r^2}\)
Minimimum occurs when \(\frac{dA}{dr}=0\)
\(\frac{10\pi r}{3}-\frac{90 \pi}{r^2}=0\)
\(\frac{10\pi r}{3}=\frac{90 \pi}{r^2}\)
\(r^3=27\)
r = 3
\(h=\frac{45}{3^2}-\frac{2}{3} \times 3\)
h = 5 - 2
h = 3
We can verify that this gives the minimum value by finding the 2nd derivative
\(\frac{dA}{dr}=\frac{10\pi r}{3}-\frac{90 \pi}{r^2}\)
\(\frac{d^2A}{dr^2}=\frac{180 \pi}{r^3}\)
When r = 3, \(\frac{d^2A}{dr^2}>0\) , hence A is a minimum












 Video Solution
Video Solution
 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn