Question 1

Marks: 5

Consider the first-order differential equation

$\frac{d y}{d x} - x^{3} = 2 \sin x$

Solve the equation given that $y = 0$ when $x = 0$ , giving your answer in the form $y = f (x)$ .

Key Concepts

Finding the Constant of Integration
Integrating Powers of x

Question 2a

Marks: 4

Use separation of variables to solve each of the following differential equations:

(a)

\frac{d y}{d x} = 10 x^{3} y^{3}

Key Concepts

Separation of Variables

Question 2b

Marks: 5

(b)

\frac{d y}{d x} = x {(x^{2} - 1)}^{3} e^{3 y}

Key Concepts

Separation of Variables

Question 3a

Marks: 5

Use separation of variables to solve each of the following differential equations for $y$ which satisfies the given boundary condition:

(a)

\frac{d y}{d x} = \frac{\cos 3 x}{y}; y (\frac{π}{6}) = - 1

Key Concepts

Separation of Variables
Finding the Constant of Integration

Question 3b

Marks: 5

(b)

e^{2 x} \frac{d y}{d x} = \cos^{2} y; y (0) = \frac{π}{4}

Key Concepts

Separation of Variables
Finding the Constant of Integration

Question 4a

Marks: 5

Radiangast the Beige is chief mathemagician of the wizards’ council. After animals begin falling ill in the forest where he lives, Radiangast realises that an evil magic has begun spreading through the forest. After studying the situation, he believes that at any point in time, $t$ , the rate of change of the area, $A$ , affected by the evil magic is inversely proportional to the square root of the area already affected.

a)

Write down a differential equation representing Radiangast’s model, and solve it to find the general solution. Be sure to define any constants that occur in your equation or solution.

Key Concepts

Modelling with Differential Equations
Separation of Variables

Question 4b

Marks: 6

At the time when Radiangast first noticed its presence, the evil magic was affecting an area of 16 acres of forest. One week later he noticed that the area has increased to 41 acres.

Radiangast knows that as long as the wizards’ council convenes to weave spells before the area affected by the evil magic exceeds 100 acres, then they will be able to stop the evil magic from spreading further.

b)

From the time that Radiangast first noticed the presence of the evil magic, determine how long the wizards’ council has to convene to weave spells, if they are to stop the evil magic from spreading further.

Key Concepts

Modelling with Differential Equations
Finding the Constant of Integration

Question 5a

Marks: 8

After an invasive species of insect has been introduced to a new region, it is estimated that at any point in time the rate of growth of the population of insects in the region will be proportional to the current population size $P$ . At the start of a study of the insects in a particular region, researchers estimate the population size to be 1000 individuals. A week later another population survey is conducted, and the population of insects is found to have increased to 1150.

(a)

By first writing and solving an appropriate differential equation, determine how long it will take for the population of insects in the region to increase to 10 000.

Key Concepts

Modelling with Differential Equations
Separation of Variables

Question 5b

Marks: 2

(b)

Comment on the validity of the model for large values of

t

.

Key Concepts

Limits
Modelling with Differential Equations

Question 6a

Marks: 3

The graph below shows the slope field for the differential equation $\frac{d y}{d x} = \frac{(0.2 x - 0.85) y}{(0.75 - 0.2 y) x},$ $x > 0, y > 0,$ in the intervals $0 < x \leq 10$ and $0 < y \leq 10$ .

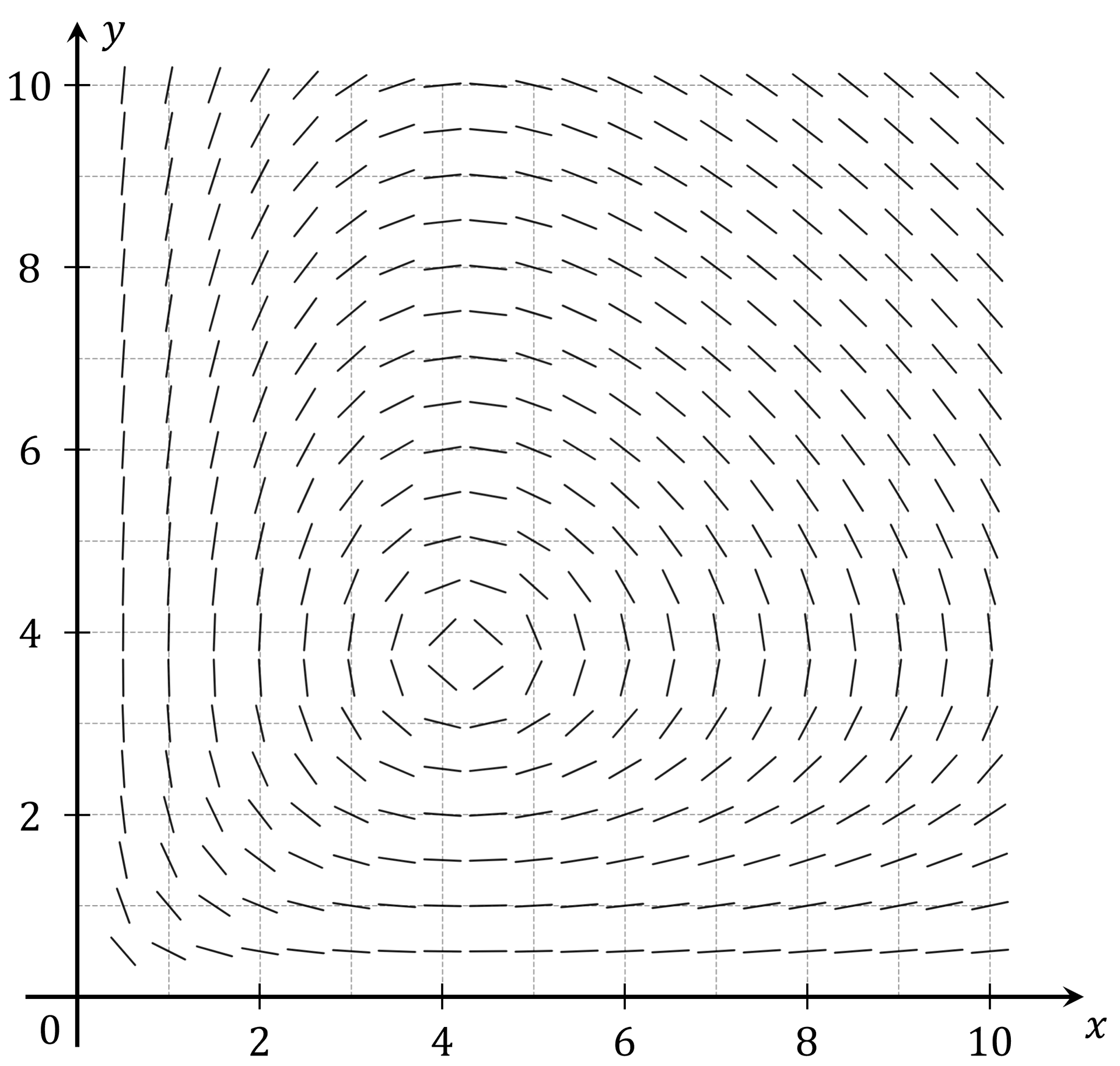
mi_q6a_5-6_differential-equations_hard_ib_ai_hl_maths_dig

a)

Find the equations of the lines on which will lie the points where the solution curves to the differential equation have (i) horizontal and (ii) vertical tangents.

Key Concepts

Tangents & Normals

Question 6b

Marks: 5

b)

On the graph above sketch:

i)

the lines identified in part (a)

ii)

the solution curve that passes through the point (8, 6)

iii)

the solution curve that passes through the point (4, 6)

Key Concepts

Slope Fields

Question 7a

Marks: 3

Consider the differential equation

$\frac{d y}{d x} = {(\frac{1}{e^{\sqrt{x}} \cos x})}^{2} - \frac{y}{\sqrt{x}}$

with the boundary condition $y (\frac{π}{3}) = 0$ .

(a)

Apply Euler’s method with a step size of

h = 0.01

to approximate the solution to the differential equation at

x = \frac{20 π + 3}{60}

.

Key Concepts

Euler's Method: First Order

Question 7b

Marks: 7

It can be shown that the exact solution to the differential equation with the given boundary condition is

$y = \frac{\tan x - \sqrt{3}}{e^{\sqrt[2]{x}}}$

b)

i)

Compare your approximation from part (a) to the exact value of the solution at

x = \frac{20 π + 3}{60}

.

ii)

Explain how the accuracy of the approximation in part (a) could be improved.

Key Concepts

Integrating Factor
Integrating with Reciprocal Trigonometric Functions

Question 7c

Marks: 3

(c)

(i)

Compare your approximation from part (a) to the exact value of the solution at

x = \frac{20 π + 3}{60}

.

(ii)

Explain how the accuracy of the approximation in part (a) could be improved.

Key Concepts

Euler's Method: First Order

Question 8a

Marks: 3

A particle moves in a straight line, such that its displacement $x$ at time $t$ is described by the differential equation

$x = \frac{t \sin t^{2}}{\cos x}, t \geq 0$

At time $t = 0, x = - \frac{π}{3}$

a)

By using Euler’s method with a step length of 0.2, find an approximate value for

x

at time

t = 0.6

.

Key Concepts

Euler's Method: First Order

Question 8b

Marks: 5

b)

Solve the differential equation with the given boundary condition.

Key Concepts

Separation of Variables
Finding the Constant of Integration

Question 8c

Marks: 2

c)

Hence find the percentage error in your approximation for

x

at time

t = 0.6 .

Key Concepts

Percentage Error

DP IB Maths: AI HL

Topic Questions

5.6 Differential Equations

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Resources

Members

Company

Quick Links