3.8 Vector Equations of Lines

1 2a 2b 3a 3b 4 5a 5b 6a 6b 7a 7b 7c 8a 8b 9a 9b 10a 10b

Question 1

Marks: 7

The line $l$ has equation $r = (\begin{matrix} 4 \\ 0 \\ 3 \end{matrix}) + λ (\begin{matrix} - 1 \\ - 2 \\ 5 \end{matrix})$ and point A has coordinates $(3, t, 2)$ . Given that the shortest distance between point A and the line is $\frac{\sqrt{645}}{15}$ units, find $t$ , where $t \in ℤ$ .

Key Concepts

Equation of a Line in Vector Form
Shortest Distance Between a Point and a Line

Question 2a

Marks: 6

A line $l_{1}$ has the equation $r_{1} = (2 + λ) i + (6 λ - 3) j + (5 + 2 λ) k$ and intersects the line $l_{2}$ with equation $r_{2} = 5 i + (7 - 4 μ) j + (- 3 - 7 μ) k$ at point P, when $λ = 3$ .

A third line $l_{3}$ runs parallel to $l_{1}$ and also intersects $l_{2}$ at point $X (t, t - 2, - 2 t)$ .

(a)

Find the parametric equations of

l_{3}

Key Concepts

Coincident, Parallel, Intersecting & Skew Lines
Equation of a Line in Parametric Form

Question 2b

Marks: 2

(b)

Find the distance

|PX|

Key Concepts

Magnitude of a Vector

Question 3a

Marks: 4

Consider the two intersecting lines $l_{1}$ and $l_{2}$ defined by the equations:

$l_{1} : r = (\begin{matrix} 9 \\ 18 \\ 11 \end{matrix}) + λ (\begin{matrix} - 6 \\ - 3 \\ k \end{matrix})$

$l_{2} : \{\begin{cases} x = 2 μ - 5 \\ y = - 4 μ - t \\ z = 3 μ + 20 \end{cases}$

Given that the angle between

l_{1}

and

l_{2}

is 1.281 radians, correct to 4 significant figures, find the value of

k

, where

k \in ℤ

Key Concepts

Angle Between Two Lines
Equation of a Line in Parametric Form

Question 3b

Marks: 3

Find the value of

t

, giving your answer correct to 3 significant figures.

Key Concepts

Equation of a Line in Vector Form

Question 4

Marks: 8

Consider the two lines $l_{1}$ and $l_{2}$ , where $l_{1}$ passes through the points $A (11, - 2, 3)$ and $B (4, 4, - 5)$ and $l_{2}$ is defined by the Parametric equations:

$l_{2} : \{\begin{cases} x = 3 μ - 7 \\ 2 y = 6 μ - 9 \\ z = - 4 μ - 4 \end{cases}$

Find the shortest distance between the two lines.

Key Concepts

Equation of a Line in Parametric Form
Shortest Distance Between Two Lines

Question 5a

Marks: 6

Consider the line $l_{1}$ as defined by the equation $r_{1} = (\begin{matrix} - 2 \\ 5 \\ - 8 \end{matrix}) + α (\begin{matrix} 2 \\ - 1 \\ 3 \end{matrix})$ .

A point $P (r, t, - r)$ lies at a distance of $\sqrt{405}$ units perpendicular from a point $X (17, 15, - 8)$ on $l_{1}$ .

Find all possible coordinates of P.

Key Concepts

Perpendicular Vectors
Magnitude of a Vector

Question 5b

Marks: 6

Given that

t > 0

, write down the set of parametric equations that defines the line

l_{2}

that passes through points P and X.

Key Concepts

Perpendicular Vectors
Magnitude of a Vector

Question 6a

Marks: 2

A wheelchair ramp is required to provide access to a building with a door that is located 22 cm above ground level. The maximum angle that a ramp must be from the horizontal is 4.8°.

(a)

Calculate the minimum horizontal distance that the ramp must extend out.

Key Concepts

Right-Angled Trigonometry

Question 6b

Marks: 8

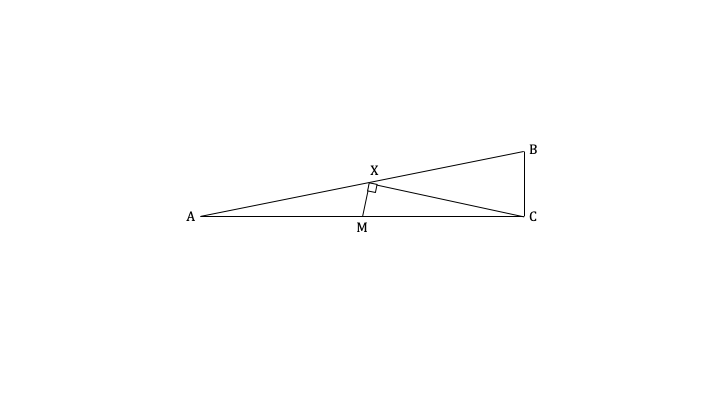
The wheelchair ramp is supported by a steel frame. A cross section of the ramp can be seen in the diagram below. A metal strut joins M, the midpoint of [AC], to a point X on the line [AB]. [AB].XM=11.1 cm and $M \hat{X} C$ =90°.

q6a_3-10_vector-equations-of-lines_very-hard_ib_aa_hl_maths-diagram

(b)

Using the horizontal distance found in part (a) and assuming that point A is at the origin, use a vector method to calculate the length XB.

Key Concepts

Perpendicular Vectors

Question 7a

Marks: 4

Some children are watching a canal boat navigating a system of locks. The boat starts at coordinates $(- 10, - 2, - 7)$ relative to the point at which the children are standing.

The $x$ direction is due east, the $y$ direction is due north and the $z$ direction is vertically upwards. All distances are measured in metres and the children are taken to be standing at the origin.

The boat travels with direction vector $1.5 i + 2 j$ for 10 metres to get into the lock and then descends vertically downwards in the lock for 11 metres before continuing along the same direction vector as it was travelling along before entering the lock.

Find the coordinates of the entrance of the lock, given that the boat is now closer to the children.

Key Concepts

Equation of a Line in Vector Form
3D Coordinate Geometry

Question 7b

Marks: 2

Find the equation of the line along which the boat is travelling after it leaves the lock

Key Concepts

Displacement Vectors
Equation of a Line in Vector Form

Question 7c

Marks: 4

On the next part of the journey at the point when the boat is closest to the children a child throws a flower to the boat driver. Given that the flower travels in a straight line and is caught by the boat driver, find the distance that the flower travelled.

Key Concepts

Shortest Distance Between a Point and a Line

Question 8a

Marks: 4

Consider the tetrahedron ABCD, where $A (3, 5, 8)$ , $B (- 2, 3, 2)$ , $C (5, - 1, 3)$ and $D (- 3, 0, 1)$ . M is the midpoint of the line $BC$ and point $P$ lies along the line $DM$ .

Given that the volume of the tetrahedron ABCP is

\frac{1}{3}

of the volume of the tetrahedron ABCD, find the Vector equation of the line going through points A and P.

Key Concepts

Equation of a Line in Vector Form
Displacement Vectors

Question 8b

Marks: 5

X is the midpoint of $[AD]$ .

Find the coordinates of the point of intersection between the line found in part (a) and the line going through

[MX]

Key Concepts

Systems of Linear Equations

Question 9a

Marks: 5

An adventure park structure is made out of steel rods arranged into a frame. As a part of the structure a red rod joins the coordinates $(2, - 26, 21)$ to $(- 6, 14, - 23)$ and a blue rod joins $(16, - 33, - 46)$ to $(6, - 18, - 21)$ .

Find the coordinates of the point where the red and blue rods meet each other.

Key Concepts

Equation of a Line in Vector Form
3D Coordinate Geometry

Question 9b

Marks: 4

The red rod also meets a yellow rod which has the vector equation $r = (s - 1) i + (s - 29) j + (8 s - 3) k$ . The point intersection of the red and blue rods and the red and yellow rods are joined by a taut rope.

Find the length of the rope.

Key Concepts

3D Coordinate Geometry
Equation of a Line in Vector Form

Question 10a

Marks: 4

A graphics designer joins the coordinates $A (1, 2, 3)$ to $B (1, 0, 1)$ and also plots the line $l$ with parametric equations:

$l : \{\begin{cases} x = 3 - 2 λ \\ y = λ - 6 \\ z = 1 - λ \end{cases}$

Find a Vector equation of the line joining the points

A

and

B

and show that it does not intersect the line

l

Key Concepts

Equation of a Line in Vector Form

Question 10b

Marks: 7

Find the two possible coordinates of the point

C

l

such that the angle

B A C

is equal to

\frac{π}{3}

radians.

Key Concepts

Angle Between Two Lines
Equation of a Line in Parametric Form

DP IB Maths: AI HL

Topic Questions

3.8 Vector Equations of Lines

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Key Concepts

Resources

Members

Company

Quick Links