IB Questionbank

Updates to Questionbank

User interface language: English | Español

Date	May 2017	Marks available	8	Reference code	17M.1.SL.TZ1.S_9
Level	Standard Level	Paper	Paper 1 (with calculator from previous syllabus)	Time zone	Time zone 1
Command term	Find	Question number	S_9	Adapted from	N/A

Question

A quadratic function $f$ can be written in the form $f(x) = a(x - p)(x - 3)$ . The graph of $f$ has axis of symmetry $x = 2.5$ and $y$ -intercept at $(0,{\text{ }} - 6)$

Find the value of $p$ .

[3]

a.

Find the value of $a$ .

[3]

b.

The line $y = kx - 5$ is a tangent to the curve of $f$ . Find the values of $k$ .

[8]

c.

Markscheme

METHOD 1 (using x-intercept)

determining that 3 is an $x$ -intercept (M1)

eg 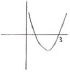$\,\,\,\,\,$ $x - 3 = 0$ , M17/5/MATME/SP1/ENG/TZ1/09.a/M

valid approach (M1)

eg $\,\,\,\,\,$ $3 - 2.5,{\text{ }}\frac{{p + 3}}{2} = 2.5$

$p = 2$ A1 N2

METHOD 2 (expanding f (x))

correct expansion (accept absence of $a$ ) (A1)

eg $\,\,\,\,\,$ $a{x^2} - a(3 + p)x + 3ap,{\text{ }}{x^2} - (3 + p)x + 3p$

valid approach involving equation of axis of symmetry (M1)

eg $\,\,\,\,\,$ $\frac{{ - b}}{{2a}} = 2.5,{\text{ }}\frac{{a(3 + p)}}{{2a}} = \frac{5}{2},{\text{ }}\frac{{3 + p}}{2} = \frac{5}{2}$

$p = 2$ A1 N2

METHOD 3 (using derivative)

correct derivative (accept absence of $a$ ) (A1)

eg $\,\,\,\,\,$ $a(2x - 3 - p),{\text{ }}2x - 3 - p$

valid approach (M1)

eg $\,\,\,\,\,$ $f’(2.5) = 0$

$p = 2$ A1 N2

[3 marks]

a.

attempt to substitute $(0,{\text{ }} - 6)$ (M1)

eg $\,\,\,\,\,$ $- 6 = a(0 - 2)(0 - 3),{\text{ }}0 = a( - 8)( - 9),{\text{ }}a{(0)^2} - 5a(0) + 6a = - 6$

correct working (A1)

eg $\,\,\,\,\,$ $- 6 = 6a$

$a = - 1$ A1 N2

[3 marks]

b.

METHOD 1 (using discriminant)

recognizing tangent intersects curve once (M1)

recognizing one solution when discriminant = 0 M1

attempt to set up equation (M1)

eg $\,\,\,\,\,$ $g = f,{\text{ }}kx - 5 = - {x^2} + 5x - 6$

rearranging their equation to equal zero (M1)

eg $\,\,\,\,\,$ ${x^2} - 5x + kx + 1 = 0$

correct discriminant (if seen explicitly, not just in quadratic formula) A1

eg $\,\,\,\,\,$ ${(k - 5)^2} - 4,{\text{ }}25 - 10k + {k^2} - 4$

correct working (A1)

eg $\,\,\,\,\,$ $k - 5 = \pm 2,{\text{ }}(k - 3)(k - 7) = 0,{\text{ }}\frac{{10 \pm \sqrt {100 - 4 \times 21} }}{2}$

$k = 3,{\text{ }}7$ A1A1 N0

METHOD 2 (using derivatives)

attempt to set up equation (M1)

eg $\,\,\,\,\,$ $g = f,{\text{ }}kx - 5 = - {x^2} + 5x - 6$

recognizing derivative/slope are equal (M1)

eg $\,\,\,\,\,$ $f’ = {m_T},{\text{ }}f' = k$

correct derivative of $f$ (A1)

eg $\,\,\,\,\,$ $- 2x + 5$

attempt to set up equation in terms of either $x$ or $k$ M1

eg $\,\,\,\,\,$ $( - 2x + 5)x - 5 = - {x^2} + 5x - 6,{\text{ }}k\left( {\frac{{5 - k}}{2}} \right) - 5 = - {\left( {\frac{{5 - k}}{2}} \right)^2} + 5\left( {\frac{{5 - k}}{2}} \right) - 6$

rearranging their equation to equal zero (M1)

eg $\,\,\,\,\,$ ${x^2} - 1 = 0,{\text{ }}{k^2} - 10k + 21 = 0$

correct working (A1)

eg $\,\,\,\,\,$ $x = \pm 1,{\text{ }}(k - 3)(k - 7) = 0,{\text{ }}\frac{{10 \pm \sqrt {100 - 4 \times 21} }}{2}$

$k = 3,{\text{ }}7$ A1A1 N0

[8 marks]

c.

Examiners report

[N/A]

a.

[N/A]

b.

[N/A]

c.

Syllabus sections

Topic 5 —Calculus » SL 5.3—Differentiating polynomials, n E Z

Show 91 related questions

18N.2.SL.TZ0.T_6a:
Calculate the area of cloth, in cm², needed to make Haruka’s bag.
19M.2.SL.TZ2.T_5b:
Write down the $y$ -intercept of the graph of $y = f\left( x \right)$ .
SPM.1.SL.TZ0.8b:
Find the value of $a$ and the value of $b$ .
18M.2.SL.TZ1.S_1c:
Solve f '(x) = f "(x).
16N.1.SL.TZ0.S_10c:
(i) Find $h'(x)$ .

(ii) Hence, show that $h'(\pi ) = \frac{{ - 21!}}{2}{\pi ^2}$ .
16N.1.SL.TZ0.S_10b:
(i) Find the first three derivatives of $g(x)$ .

(ii) Given that ${g^{(19)}}(x) = \frac{{k!}}{{(k - p)!}}({x^{k - 19}})$ , find $p$ .
17M.2.SL.TZ2.T_6f:
Write down the number of possible solutions to the equation $f(x) = 5$ .
18M.1.AHL.TZ1.H_7a:
Find $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ .
SPM.1.SL.TZ0.8c.i:
Sketch the graph of $y = f'\left( x \right)$ .
17M.2.AHL.TZ1.H_12c:
Explain why $f$ is an even function.
17M.2.AHL.TZ1.H_12b:
Sketch the graph of $y = f(x)$ showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
16N.1.SL.TZ0.S_10a:
(i) Find the first four derivatives of $f(x)$ .

(ii) Find ${f^{(19)}}(x)$ .
SPM.1.SL.TZ0.8a:
Find $f'\left( x \right)$ .
19N.2.SL.TZ0.S_3b:
Let ${\text{C}}$ be a point on the graph of $h$ . The tangent to the graph of $h$ at ${\text{C}}$ is parallel to the graph of $f$ .

Find the $x$ -coordinate of ${\text{C}}$ .
19M.2.SL.TZ2.T_5c:
Sketch the graph of $y = f\left( x \right)$ for −3 ≤ $x$ ≤ 3 and −4 ≤ $y$ ≤ 12.
19N.2.SL.TZ0.S_3a:
Find $h\left( x \right)$ .
18N.1.SL.TZ0.S_10b.i:
Find $f'\left( x \right)$ .
16N.1.SL.TZ0.T_14b:
Find the coordinates of P.
18M.1.SL.TZ2.S_9b:
Show that $C = 20\pi {r^2} + \frac{{320\pi }}{r}$ .
19M.1.SL.TZ2.S_10c:
Write down an expression for the area of $R$ .
18N.1.SL.TZ0.S_10c:
The graph of $f$ has a local minimum at the point Q. The line L passes through Q.

Find the value of $a$ .
17M.2.AHL.TZ1.H_2a:
Find $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ in terms of $x$ and $y$ .
22M.1.SL.TZ2.7d:
Find the values of $d$ for which $g$ is an increasing function.
SPM.1.SL.TZ0.8c.ii:
Hence explain why the graph of $f$ has a local maximum point at $x = a$ .
19M.1.AHL.TZ1.H_7:
Find the coordinates of the points on the curve ${y^3} + 3x{y^2} - {x^3} = 27$ at which $\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0$ .
20N.1.SL.TZ0.T_13b:
Write down the gradient of this tangent.
SPM.1.SL.TZ0.8d.i:
Find $f''\left( b \right)$ .
17N.1.SL.TZ0.S_8d:
Find the area of the region enclosed by the graph of $f$ and the line $L$ .
17M.2.AHL.TZ1.H_8b:
Calculate $\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ when $\theta = \frac{\pi }{3}$ .
19M.1.SL.TZ2.S_10d:
Hence find the exact area of $R$ .
17M.2.AHL.TZ1.H_12d:
Explain why the inverse function ${f^{ - 1}}$ does not exist.
17M.2.AHL.TZ1.H_12g.i:
Hence, show that there are no solutions to $g'(x) = 0$ ;
17N.1.AHL.TZ0.H_7:
The folium of Descartes is a curve defined by the equation ${x^3} + {y^3} - 3xy = 0$ , shown in the following diagram.

Determine the exact coordinates of the point P on the curve where the tangent line is parallel to the $y$ -axis.
17N.2.SL.TZ0.T_5b.ii:
Find $f’(x)$ .
17M.2.AHL.TZ1.H_12a:
Find the largest possible domain $D$ for $f$ to be a function.
20N.1.SL.TZ0.S_10b:
Find the area of triangle $AOB$ in terms of $k$ .
21M.3.AHL.TZ1.1b:
Write down an expression for $f' (x)$ .
18M.1.SL.TZ1.S_7:
Consider f(x), g(x) and h(x), for x∈ $\mathbb{R}$ where h(x) = $\left( {f \circ g} \right)$ (x).

Given that g(3) = 7 , g′ (3) = 4 and f ′ (7) = −5 , find the gradient of the normal to the curve of h at x = 3.
17M.2.SL.TZ1.S_6:
Let $f(x) = {({x^2} + 3)^7}$ . Find the term in ${x^5}$ in the expansion of the derivative, $f’(x)$ .
17M.2.AHL.TZ1.H_12f:
Find $g'(x)$ .
18M.1.SL.TZ2.S_9a:
Express h in terms of r.
20N.1.SL.TZ0.S_10c:
The graph of $f$ is translated by $(\begin{matrix} 4 \\ 3 \end{matrix})$ to give the graph of $g$ .
In the following diagram:
- point $Q$ lies on the graph of $g$
- points $C$ , $D$ and $E$ lie on the vertical asymptote of $g$
- points $D$ and $F$ lie on the horizontal asymptote of $g$
- point $G$ lies on the $x$ -axis such that $FG$ is parallel to $DC$ .
Line $L_{2}$ is the tangent to the graph of $g$ at $Q$ , and passes through $E$ and $F$ .

Given that triangle $EDF$ and rectangle $CDFG$ have equal areas, find the gradient of $L_{2}$ in terms of $p$ .
19M.1.SL.TZ2.T_15c:
Hence, find the number of vases that will maximize the profit.
17M.2.AHL.TZ1.H_12e:
Find the inverse function ${g^{ - 1}}$ and state its domain.
20N.1.SL.TZ0.S_10a.ii:
Show that the equation of $L_{1}$ is $k x + p^{2} y - 2 p k = 0$ .
SPM.1.SL.TZ0.8e:
The normal to the graph of $f$ at $x = a$ and the tangent to the graph of $f$ at $x = b$ intersect at the point ( $p$ , $q$ ) .

Find the value of $p$ and the value of $q$ .
20N.1.SL.TZ0.S_10a.i:
Find $f' (p)$ in terms of $k$ and $p$ .
19M.1.SL.TZ1.T_15a:
Write down an equation for the area, $A$ , of the curved surface in terms of $r$ .
19M.1.SL.TZ2.T_15a:
Find the value of $P$ if no vases are sold.
17M.2.SL.TZ2.T_6d.i:
Write down the $x$ -coordinates of these two points;
17N.2.SL.TZ0.T_5b.i:
Expand the expression for $f(x)$ .
16N.2.SL.TZ0.T_6b:
Express this volume in ${\text{c}}{{\text{m}}^3}$ .
16N.2.SL.TZ0.T_6c:
Write down, in terms of $r$ and $h$ , an equation for the volume of this water container.
16N.2.SL.TZ0.T_6e:
Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of $r$ which minimizes $A$ .
17M.2.AHL.TZ1.H_8a:
Find an expression for the volume of water $V{\text{ }}({{\text{m}}^3})$ in the trough in terms of $\theta$ .
18N.1.SL.TZ0.S_10b.ii:
Hence, find the equation of L in terms of $a$ .
18M.1.SL.TZ2.S_9c:
Given that there is a minimum value for C, find this minimum value in terms of $\pi$ .
16N.2.AHL.TZ0.H_6:
An earth satellite moves in a path that can be described by the curve $72.5{x^2} + 71.5{y^2} = 1$ where $x = x(t)$ and $y = y(t)$ are in thousands of kilometres and $t$ is time in seconds.

Given that $\frac{{{\text{d}}x}}{{{\text{d}}t}} = 7.75 \times {10^{ - 5}}$ when $x = 3.2 \times {10^{ - 3}}$ , find the possible values of $\frac{{{\text{d}}y}}{{{\text{d}}t}}$ .

Give your answers in standard form.
SPM.1.SL.TZ0.8d.ii:
Hence, use your answer to part (d)(i) to show that the graph of $f$ has a local minimum point at $x = b$ .
17M.2.AHL.TZ1.H_2b:
Determine the equation of the tangent to $C$ at the point $\left( {\frac{2}{{\text{e}}},{\text{ e}}} \right)$
19M.1.SL.TZ2.S_10b:
Hence find $\int {\left( {3{x^2} + 1} \right)\sqrt {{x^3} + x} } \,{\text{d}}x$ .
18M.1.AHL.TZ1.H_7b:
Find $\int_0^1 {{\text{arccos}}\left( {\frac{x}{2}} \right){\text{d}}x}$ .
17M.2.AHL.TZ1.H_12g.ii:
Hence, show that there are no solutions to $({g^{ - 1}})'(x) = 0$ .
16N.1.SL.TZ0.T_14a:
Find $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ .
18M.1.AHL.TZ2.H_6b:
Hence, or otherwise, find $\int\limits_0^\pi {{{\text{e}}^{ - x}}\,{\text{sin}}\,x\,{\text{d}}x}$ .
18N.2.SL.TZ0.T_6g:
Use your answer to part (f) to show that the width of Nanako’s bag is 12 cm.
19M.1.SL.TZ1.T_15c:
Find the value of $r$ when the area of the curved surface is maximized.
18N.2.SL.TZ0.T_6d:
Write down and simplify an expression in x and y for the area of cloth, A, used to make Nanako’s bag.
19M.1.SL.TZ2.T_15b:
Differentiate $P\left( x \right)$ .
20N.1.SL.TZ0.T_13c:
Find the value of $k$ .
17M.2.SL.TZ2.T_6a:
Write down the $y$ -intercept of the graph.
17M.2.SL.TZ2.T_6c.i:
Show that $a = 8$ .
17M.2.SL.TZ2.T_6b:
Find $f'(x)$ .
20N.1.SL.TZ0.T_13a:
Write down $f' (x)$ .
19M.2.SL.TZ2.T_5h:
Determine the range of $f\left( x \right)$ for $p$ ≤ $x$ ≤ $q$ .
17N.2.SL.TZ0.T_5e:
Write down the coordinates of the point of intersection.
17M.2.SL.TZ2.T_6g:
The equation $f(x) = m$ , where $m \in \mathbb{R}$ , has four solutions. Find the possible values of $m$ .
16N.2.SL.TZ0.T_6d:
Show that $A = \pi {r^2} + \frac{{1\,000\,000}}{r}$ .
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
19M.1.SL.TZ1.T_15b:
Find $\frac{{{\text{d}}A}}{{{\text{d}}r}}$ .
18N.2.SL.TZ0.T_6e:
Use your answers to parts (c) and (d) to show that

$A = 3{x^2} + \frac{{10368}}{x}$ .
16N.2.SL.TZ0.T_6a:
Write down a formula for $A$ , the surface area to be coated.
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
17N.2.SL.TZ0.T_5d:
Draw the graph of $f$ for $- 3 \leqslant x \leqslant 3$ and $- 40 \leqslant y \leqslant 20$ . Use a scale of 2 cm to represent 1 unit on the $x$ -axis and 1 cm to represent 5 units on the $y$ -axis.
17M.2.SL.TZ2.T_6c.ii:
Find $f(2)$ .
17M.2.SL.TZ2.T_6d.ii:
Write down the intervals where the gradient of the graph of $y = f(x)$ is positive.
17M.2.SL.TZ2.T_6e:
Write down the range of $f(x)$ .
18N.2.SL.TZ0.T_6b:
Calculate the volume, in cm³, of the bag.
18N.2.SL.TZ0.T_6c:
Use this value to write down, and simplify, the equation in x and y for the volume of Nanako’s bag.
18N.2.SL.TZ0.T_6f:
Find $\frac{{{\text{d}}A}}{{{\text{d}}x}}$ .

Hide related questions

Topic 5 —Calculus » SL 5.4—Tangents and normal

Topic 2—Functions » SL 2.7—Solutions of quadratic equations and inequalities, discriminant and nature of roots

Topic 2—Functions

Topic 5 —Calculus