| Date | May 2017 | Marks available | 2 | Reference code | 17M.2.SL.TZ2.T_6 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Find | Question number | T_6 | Adapted from | N/A |
Question
Consider the function , where is a constant. Part of the graph of is shown below.
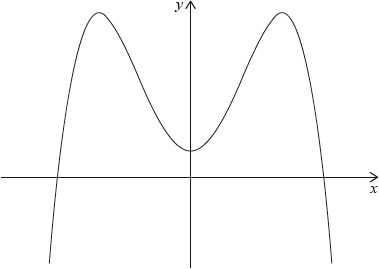
It is known that at the point where the tangent to the graph of is horizontal.
There are two other points on the graph of at which the tangent is horizontal.
Write down the -intercept of the graph.
Find .
Show that .
Find .
Write down the -coordinates of these two points;
Write down the intervals where the gradient of the graph of is positive.
Write down the range of .
Write down the number of possible solutions to the equation .
The equation , where , has four solutions. Find the possible values of .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
5 (A1)
Note: Accept an answer of .
[1 mark]
(A1)(A1)
Note: Award (A1) for and (A1) for . Award at most (A1)(A0) if extra terms are seen.
[2 marks]
(M1)(M1)
Note: Award (M1) for substitution of into their derivative, (M1) for equating their derivative, written in terms of , to 0 leading to a correct answer (note, the 8 does not need to be seen).
(AG)
[2 marks]
(M1)
Note: Award (M1) for correct substitution of and into the formula of the function.
21 (A1)(G2)
[2 marks]
(A1)(A1)
Note: Award (A1) for each correct solution. Award at most (A0)(A1)(ft) if answers are given as and or and .
[2 marks]
(A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for , follow through from part (d)(i) provided their value is negative.
Award (A1)(ft) for , follow through only from their 0 from part (d)(i); 2 must be the upper limit.
Accept interval notation.
[2 marks]
(A1)(ft)(A1)
Notes: Award (A1)(ft) for 21 seen in an interval or an inequality, (A1) for “”.
Accept interval notation.
Accept or .
Follow through from their answer to part (c)(ii). Award at most (A1)(ft)(A0) if is seen instead of . Do not award the second (A1) if a (finite) lower limit is seen.
[2 marks]
3 (solutions) (A1)
[1 mark]
or equivalent (A1)(ft)(A1)
Note: Award (A1)(ft) for 5 and 21 seen in an interval or an inequality, (A1) for correct strict inequalities. Follow through from their answers to parts (a) and (c)(ii).
Accept interval notation.
[2 marks]

