IB Questionbank

User interface language: English | Español

Date	May 2017	Marks available	3	Reference code	17M.2.AHL.TZ1.H_12
Level	Additional Higher Level	Paper	Paper 2	Time zone	Time zone 1
Command term	Sketch	Question number	H_12	Adapted from	N/A

Question

Consider $f(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right)$

The function $f$ is defined by $f(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right),{\text{ }}x \in D$

The function $g$ is defined by $g(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right),{\text{ }}x \in \left] {1,{\text{ }}\infty } \right[$ .

Find the largest possible domain $D$ for $f$ to be a function.

[2]

Sketch the graph of $y = f(x)$ showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.

[3]

Explain why $f$ is an even function.

[1]

Explain why the inverse function ${f^{ - 1}}$ does not exist.

[1]

Find the inverse function ${g^{ - 1}}$ and state its domain.

[4]

Find $g'(x)$ .

[3]

Hence, show that there are no solutions to $g'(x) = 0$ ;

[2]

g.i.

Hence, show that there are no solutions to $({g^{ - 1}})'(x) = 0$ .

[2]

g.ii.

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

${x^2} - 1 > 0$ (M1)

$x < - 1$ or $x > 1$ A1

[2 marks]

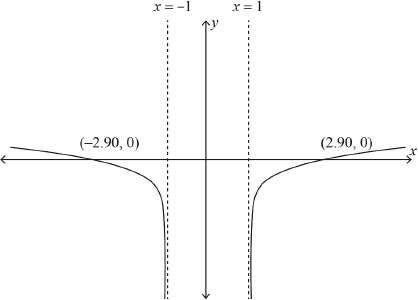
M17/5/MATHL/HP2/ENG/TZ1/12.b/M

shape A1

$x = 1$ and $x = - 1$ A1

$x$ -intercepts A1

[3 marks]

EITHER

$f$ is symmetrical about the $y$ -axis R1

$f( - x) = f(x)$ R1

[1 mark]

EITHER

$f$ is not one-to-one function R1

horizontal line cuts twice R1

Note: Accept any equivalent correct statement.

[1 mark]

$x = - 1 + \ln \left( {\sqrt {{y^2} - 1} } \right)$ M1

${{\text{e}}^{2x + 2}} = {y^2} - 1$ M1

${g^{ - 1}}(x) = \sqrt {{{\text{e}}^{2x + 2}} + 1} ,{\text{ }}x \in \mathbb{R}$ A1A1

[4 marks]

$g'(x) = \frac{1}{{\sqrt {{x^2} - 1} }} \times \frac{{2x}}{{2\sqrt {{x^2} - 1} }}$ M1A1

$g'(x) = \frac{x}{{{x^2} - 1}}$ A1

[3 marks]

$g'(x) = \frac{x}{{{x^2} - 1}} = 0 \Rightarrow x = 0$ M1

which is not in the domain of $g$ (hence no solutions to $g'(x) = 0$ ) R1

[2 marks]

g.i.

$({g^{ - 1}})'(x) = \frac{{{{\text{e}}^{2x + 2}}}}{{\sqrt {{{\text{e}}^{2x + 2}} + 1} }}$ M1

as ${{\text{e}}^{2x + 2}} > 0 \Rightarrow ({g^{ - 1}})'(x) > 0$ so no solutions to $({g^{ - 1}})'(x) = 0$ R1

Note: Accept: equation ${{\text{e}}^{2x + 2}} = 0$ has no solutions.

[2 marks]

g.ii.

Examiners report

[N/A]

g.i.

[N/A]

g.ii.

Syllabus sections

Topic 2—Functions » SL 2.2—Functions, notation domain, range and inverse as reflection

Show 83 related questions

22M.1.SL.TZ2.1a:
Find $g (0)$ .
22M.1.SL.TZ2.1c:
Find the value of $x$ such that $f (x) = 0$ .
18N.2.AHL.TZ0.H_9c.i:
sketch the graph of $y = f\left( x \right)$ , showing clearly any axis intercepts and giving the equations of any asymptotes.
21N.1.AHL.TZ0.2a.i:
the vertical asymptote of the graph of $f$ .
21N.1.AHL.TZ0.2a.ii:
the horizontal asymptote of the graph of $f$ .
21N.1.AHL.TZ0.2c:
Sketch the graph of $f$ on the axes below.
18M.1.SL.TZ1.T_15b:
Write down the x-coordinate of P and the x-coordinate of Q.
19M.2.SL.TZ2.T_5b:
Write down the $y$ -intercept of the graph of $y = f\left( x \right)$ .
19M.2.AHL.TZ1.H_4a:
Write down the range of $f$ .
17M.1.AHL.TZ2.H_2a:
Write down the range of $f$ .
16N.2.AHL.TZ0.H_5c:
Solve the inequality $\left| {3x\arccos (x)} \right| > 1$ .
17M.1.SL.TZ1.T_12b.ii:
Write down the number of solutions to $f(x) = - 6$ .
17M.2.AHL.TZ1.H_12c:
Explain why $f$ is an even function.
19N.1.SL.TZ0.S_10c:
The line ${L_2}$ is tangent to the graph of $g$ at ${\text{A}}$ and has equation $y = \left( {{\text{ln}}\,p} \right)x + q + 1$ .

The line ${L_2}$ passes through the point $\left( { - 2{\text{, }} - 2} \right)$ .

The gradient of the normal to $g$ at ${\text{A}}$ is $\frac{1}{{{\text{ln}}\left( {\frac{1}{3}} \right)}}$ .

Find the equation of ${L_1}$ in terms of $x$ .
18M.1.SL.TZ1.T_15c:
Write down the values of x for which $f\left( x \right) > g\left( x \right)$ .
21N.1.AHL.TZ0.2b.ii:
the $y$ -axis.
19M.2.SL.TZ1.T_4a:
Find the value of $f\left( x \right)$ when $x = \frac{1}{2}$ .
19N.1.SL.TZ0.S_10a:
Write down the coordinates of ${\text{B}}$ .
18N.2.AHL.TZ0.H_9c.ii:
sketch the graph of $y = {f^{ - 1}}\left( x \right)$ , showing clearly any axis intercepts and giving the equations of any asymptotes.
19M.2.SL.TZ2.T_5c:
Sketch the graph of $y = f\left( x \right)$ for −3 ≤ $x$ ≤ 3 and −4 ≤ $y$ ≤ 12.
19N.2.AHL.TZ0.H_3b:
Given that ${f^{ - 1}}\left( a \right) = 3$ , determine the value of $a$ .
17M.1.AHL.TZ2.H_2b:
Find an expression for ${f^{ - 1}}(x)$ .
EXN.1.SL.TZ0.8c:
Find an expression for $f^{- 1} (x)$ , stating its domain.
22M.1.AHL.TZ2.6b:
The range of $f$ is $a \leq y \leq b$ , where $a, b \in ℝ$ .

Find the value of $a$ and the value of $b$ .
17M.2.SL.TZ2.S_3a:
Write down the range of $f$ .
22M.2.AHL.TZ1.10b.ii:
State the domain and range of $f^{- 1}$ .
22M.2.AHL.TZ2.10a.ii:
Plant $A$ correct to three significant figures.
19N.2.AHL.TZ0.H_3c:
Given that $g\left( x \right) = 2f\left( {x - 1} \right)$ , find the domain and range of $g$ .
20N.1.AHL.TZ0.H_10a.i:
Write down an expression for $f' (x)$ .
20N.1.AHL.TZ0.H_10b.i:
Show that $g^{- 1}$ exists.
20N.1.AHL.TZ0.H_12b:
State the equation of the horizontal asymptote on the graph of $y = f (x)$ .
20N.1.AHL.TZ0.H_12d:
Sketch the graph of $y = f (x)$ , stating clearly the equations of any asymptotes and the coordinates of any points of intersections with the coordinate axes.
20N.1.SL.TZ0.T_2a.ii:
State, in the context of the question, what the value of $8.50$ represents.
20N.1.SL.TZ0.T_2b:
Write down the minimum number of pizzas that can be ordered.
19N.2.AHL.TZ0.H_3a:
Find the value of $\left( {f \circ f} \right)\left( 1 \right)$ .
18M.1.SL.TZ1.T_15a:
Find the range of f.
18N.2.AHL.TZ0.H_9d:
Hence, or otherwise, solve the inequality $f\left( x \right) > {f^{ - 1}}\left( x \right)$ .
21M.2.SL.TZ1.9e:
The line $L$ is tangent to the graphs of both $f$ and the inverse function $f^{- 1}$ .

Find the shaded area enclosed by the graphs of $f$ and $f^{- 1}$ and the line $L$ .
16N.2.AHL.TZ0.H_5b:
State the range of $f$ .
17M.2.AHL.TZ1.H_12d:
Explain why the inverse function ${f^{ - 1}}$ does not exist.
17M.2.AHL.TZ1.H_12g.i:
Hence, show that there are no solutions to $g'(x) = 0$ ;
20N.1.AHL.TZ0.H_10b.iii:
Hence find $g^{- 1} (x)$ .
20N.1.AHL.TZ0.H_10a.ii:
Hence, given that $f^{- 1}$ does not exist, show that $b^{2} - 3 a c > 0$ .
17M.2.AHL.TZ1.H_12a:
Find the largest possible domain $D$ for $f$ to be a function.
17M.2.AHL.TZ1.H_12f:
Find $g'(x)$ .
16N.2.AHL.TZ0.H_5a:
Sketch the graph of $f$ indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.
17M.1.SL.TZ1.T_12b.i:
Draw the line $y = - 6$ on the axes.
19N.1.SL.TZ0.S_10b:
Given that $f'\left( a \right) = \frac{1}{{{\text{ln}}\,p}}$ , find the equation of ${L_1}$ in terms of $x$ , $p$ and $q$ .
EXN.1.SL.TZ0.8b:
State the range of $f$ .
17M.2.AHL.TZ1.H_12e:
Find the inverse function ${g^{ - 1}}$ and state its domain.
21M.2.SL.TZ2.5a:
Find the range of $f$ .
17M.2.SL.TZ2.S_3c:
Write down the domain of $g$ .
21N.1.AHL.TZ0.2d:
The function $g$ is defined by $g (x) = \frac{a x + 4}{3 - x}$ , where $x \in ℝ, x \neq 3$ and $a \in ℝ$ .

Given that $g (x) = g^{- 1} (x)$ , determine the value of $a$ .
22M.1.AHL.TZ2.11a:
Sketch the curve $y = f (x)$ , clearly indicating any asymptotes with their equations. State the coordinates of any local maximum or minimum points and any points of intersection with the coordinate axes.
22M.2.AHL.TZ2.10a.i:
Plant $B$ .
21N.1.AHL.TZ0.2b.i:
the $x$ -axis.
16N.1.SL.TZ0.T_9b:
Find the value of $b$ .
16N.1.SL.TZ0.T_9c:
Write down the range of $f(x)$ .
17M.1.SL.TZ1.T_12c:
Find the range of values of $k$ for which $f(x) = k$ has no solution.
20N.1.AHL.TZ0.H_10b.ii:
$g (x)$ can be written in the form $p (x - 2)^{3} + q$ , where $p, q \in ℝ$ .

Find the value of $p$ and the value of $q$ .
20N.1.AHL.TZ0.H_10d:
Sketch the graphs of $y = g (x)$ and $y = g^{- 1} (x)$ on the same set of axes, indicating the points where each graph crosses the coordinate axes.
20N.1.AHL.TZ0.H_12a:
State the equation of the vertical asymptote on the graph of $y = f (x)$ .
20N.1.AHL.TZ0.H_12c:
Use an algebraic method to determine whether $f$ is a self-inverse function.
20N.1.AHL.TZ0.H_12e:
The region bounded by the $x$ -axis, the curve $y = f (x)$ , and the lines $x = 5$ and $x = 7$ is rotated through $2 π$ about the $x$ -axis. Find the volume of the solid generated, giving your answer in the form $π (a + b \ln 2)$ , where $a, b \in ℤ$ .
17M.2.AHL.TZ1.H_12g.ii:
Hence, show that there are no solutions to $({g^{ - 1}})'(x) = 0$ .
17N.2.AHL.TZ0.H_10d:
This region is now rotated through $2\pi$ radians about the $x$ -axis. Find the volume of revolution.
19M.2.AHL.TZ1.H_4b:
Find $f'\left( x \right)$ , stating its domain.
21M.2.AHL.TZ2.12e:
State the domain of $g^{- 1}$ .
20N.1.AHL.TZ0.H_10c:
State each of the transformations in the order in which they are applied.
17N.1.SL.TZ0.S_3c:
On the grid, sketch the graph of ${f^{ - 1}}$ .
EXN.1.SL.TZ0.8d:
Find the coordinates of the point(s) where the graphs of $y = f (x)$ and $y = f^{- 1} (x)$ intersect.
18N.2.AHL.TZ0.H_9b:
Hence, or otherwise, find the coordinates of the point of inflexion on the graph of $y = f\left( x \right)$ .
17M.1.AHL.TZ2.H_2c:
Write down the domain and range of ${f^{ - 1}}$ .
17M.2.SL.TZ1.S_10a.iii:
Write down the value of $k$ .
16N.1.SL.TZ0.T_9a:
Write down the equation of the axis of symmetry for this graph.
19M.2.SL.TZ1.T_4d:
Find the distance from the centre of Orangeton to the point at which the road meets the highway.
19M.2.SL.TZ1.T_4c:
Find the coordinates of the bridges relative to the centre of Orangeton.
20N.1.SL.TZ0.T_2a.i:
State, in the context of the question, what the value of $34.50$ represents.
19M.2.SL.TZ1.T_4e:
This straight road crosses the highway and then carries on due north.

State whether the straight road will ever cross the river. Justify your answer.
20N.1.SL.TZ0.T_2c:
Kaelani has $450 PGK$ .

Find the maximum number of large cheese pizzas that Kaelani can order from Olava’s Pizza Company.
19M.2.SL.TZ1.T_4b.ii:
State the domain of $P$ .
19M.2.SL.TZ2.T_5h:
Determine the range of $f\left( x \right)$ for $p$ ≤ $x$ ≤ $q$ .
19M.2.SL.TZ1.T_4b.i:
Find the function, $P\left( x \right)$ , that would define this footpath on the map.

Hide related questions

Topic 5 —Calculus » SL 5.3—Differentiating polynomials, n E Z

Topic 2—Functions » SL 2.4—Key features of graphs, intersections using technology

Topic 5 —Calculus » SL 5.6—Differentiating polynomials n E Q. Chain, product and quotient rules

Topic 2—Functions

Topic 5 —Calculus

Question

Markscheme

Examiners report

Syllabus sections

View options