DP Chemistry Questionbank

A.8 Superconducting metals and X-ray crystallography (HL only)
Description
[N/A]Directly related questions
-
16N.3.hl.TZ0.8a:
(i) The diagram below shows the diffraction of two X-ray beams, y and z of wavelength λ, shining on a chromium crystal whose planes are a distance d nm apart.
Deduce the extra distance travelled by the second beam, z, compared to the first one, y.
(ii) State the Bragg’s condition for the observed diffraction to be at its strongest (constructive interference).
- 16N.3.hl.TZ0.9b: Outline one difference between type 1 and type 2 superconductors.
- 16N.3.hl.TZ0.9a: Describe the Meissner effect.
-
16N.3.hl.TZ0.8b:
(i) The mass of one unit cell of chromium metal is 17.28 × 10−23 g. Calculate the number of unit cells in one mole of chromium. Ar(Cr) = 52.00.
(ii) Deduce the number of atoms of chromium per unit cell.
-
17M.3.hl.TZ1.8b:
Lanthanum becomes superconducting below 5 K. Explain, in terms of Bardeen–Cooper–Schrieffer (BCS) theory, how superconductivity occurs.
-
17M.3.hl.TZ1.8a:
Lanthanum has a hexagonal close packed (hcp) crystal structure. State the coordination number of each lanthanum atom.
-
17M.3.hl.TZ1.8c:
Outline why superconductivity only occurs at low temperatures.
-
17M.3.hl.TZ2.5c.ii:
Rhodium is a type 1 superconductor.
Sketch graphs of resistance against temperature for a conductor and superconductor.
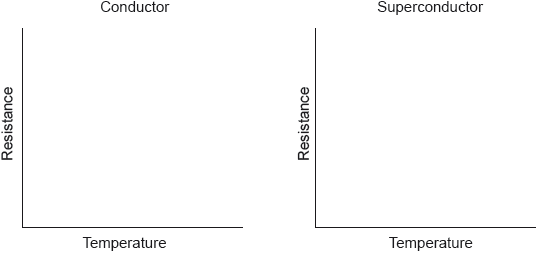
-
17M.3.hl.TZ2.5c.iii:
Contrast type 1 and type 2 superconductors by referring to three differences between them.
- 20N.3.hl.TZ0.4b(i): CNT can act as Type 2 superconductors. Outline why Type 2 superconductors are generally more...
-
20N.3.hl.TZ0.4b(ii):
Explain the role of electrons in superconducting materials in terms of the Bardeen–Cooper–Schrieffer (BCS) theory.
-
17N.3.hl.TZ0.8a:
Calculate the total number of cobalt atoms within its unit cell.
-
17N.3.hl.TZ0.6b:
Explain why Type 2 superconductors are generally more useful than Type 1.
-
17N.3.hl.TZ0.8b.i:
The atomic radius, r, of cobalt is 1.18 × 10–8 cm. Determine the edge length, in cm, of the unit cell, a, using the second diagram.
-
17N.3.hl.TZ0.8b.ii:
Determine a value for the density of cobalt, in g cm–3, using data from sections 2 and 6 of the data booklet and your answers from (a) and (b) (i).
If you did not obtain an answer to (b) (i), use 3.00 × 10–8 cm but this is not the correct answer.
-
18M.3.hl.TZ2.4a.i:
Deduce the number of atoms per unit cell in vanadium.
-
18M.3.hl.TZ1.5b:
The diagram illustrates the crystal structure of aluminium metal with the unit cell indicated. Outline the significance of the unit cell.
-
18M.3.hl.TZ1.5c:
When X-rays of wavelength 0.154 nm are directed at a crystal of aluminium, the first order diffraction pattern is observed at 18°. Determine the separation of layers of aluminium atoms in the crystal, in m, using section 1 of the data booklet.
-
18M.3.hl.TZ1.5d.i:
Deduce what the shape of the graph indicates about aluminium.
-
18M.3.hl.TZ2.4a.iii:
Calculate the average mass, in g, of a vanadium atom by using sections 2 and 6 of the data booklet.
-
18M.3.hl.TZ2.4a.ii:
Calculate the expected first order diffraction pattern angle, in degrees, if x-rays of wavelength 150 pm are directed at a crystal of vanadium. Assume the edge length of the crystal to be the same as separation of layers of vanadium atoms found by x-ray diffraction. Use section 1 of the data booklet.
-
18M.3.hl.TZ2.4a.iv:
Determine the volume, in cm3, of a vanadium unit cell.
-
18M.3.hl.TZ1.5d.ii:
Outline why the resistance of aluminium increases above 1.2 K.
-
18M.3.hl.TZ2.4a.v:
Determine the density, in g cm−3, of vanadium by using your answers to (a)(i), (a)(iii) and (a)(iv).
-
18N.3.hl.TZ0.5a.ii:
Calculate the number of atoms per unit cell of gold, showing your working.
- 18N.3.hl.TZ0.5a.i: State the name of the crystal structure of gold.
-
18N.3.hl.TZ0.5b:
The edge length of the gold unit cell is 4.08 × 10‒8 cm.
Determine the density of gold in g cm‒3, using sections 2 and 6 of the data booklet.
-
19M.3.hl.TZ1.3e:
Lithium forms a crystalline lattice with the unit cell structure shown below.
X-ray diffraction shows that the length of the edge of the unit cell is 3.51 × 10−8 cm.
Determine the density of lithium, in g cm−3, using sections 2 and 6 of the data booklet.
-
19M.3.hl.TZ1.3d(i):
Lithium has shown some superconductive properties when doped into graphene or when under high pressure. Under high pressure, however, the Meissner effect is absent.
Describe the Meissner effect.
-
19M.3.hl.TZ1.3d(ii):
At very low temperatures, lithium atoms enhance the phonon binding of electrons in graphene suggesting the formation of Cooper pairs.
Explain how Cooper pairs are formed.
-
19M.3.hl.TZ2.7a:
State what is meant by a superconductor.
-
19M.3.hl.TZ2.6a:
State the number of atoms in the unit cell.
-
19M.3.hl.TZ2.18b:
Outline one approach to controlling industrial emissions of carbon dioxide.
-
19M.3.hl.TZ2.6b:
Determine the density of calcium, in g cm−3, using section 2 of the data booklet.
Ar = 40.08; metallic radius (r) = 1.97 × 10−10 m
- 19N.3.hl.TZ0.4b: State two differences between Type I and Type II superconductors.
- 19N.3.hl.TZ0.4a(ii): Suggest why the resistance of metals increases with temperature.
- 19N.3.hl.TZ0.4a(i): Outline how resistance to electric currents occurs in metals.
-
19N.3.hl.TZ0.7:
X-ray crystallography of a metal crystal produces a diffraction pattern of bright spots.
Using X-rays of wavelength 1.54 × 10−10 m, the first bright spots were produced at an angle θ of 22.3° from the centre.
Calculate the separation between planes of atoms in the lattice, in meters, using section 1 of the data booklet.
