| Date | November 2017 | Marks available | 1 | Reference code | 17N.3.hl.TZ0.8 |
| Level | HL | Paper | 3 | Time zone | TZ0 |
| Command term | Determine | Question number | 8 | Adapted from | N/A |
Question
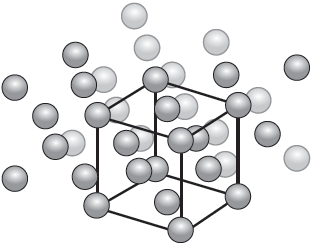
Metals have various crystal structures. Cobalt forms a face-centred cubic (FCC) lattice. Two representations of FCC are shown.
Calculate the total number of cobalt atoms within its unit cell.
The atomic radius, r, of cobalt is 1.18 × 10–8 cm. Determine the edge length, in cm, of the unit cell, a, using the second diagram.
Determine a value for the density of cobalt, in g cm–3, using data from sections 2 and 6 of the data booklet and your answers from (a) and (b) (i).
If you did not obtain an answer to (b) (i), use 3.00 × 10–8 cm but this is not the correct answer.
Markscheme
«» 4
face diagonal
«» 3.34 x 10–8 «cm»
mass of 4 atoms = «g»
«density » 10.5 «g cm–3»
Answer using 3.00 x 10–8 cm:
mass of 4 atoms = «g»
«density » 14.5 «g cm–3»
Award [2] for correct final answer.