| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.hl.TZ1.12 |
| Level | HL only | Paper | 1 | Time zone | TZ1 |
| Command term | Write down | Question number | 12 | Adapted from | N/A |
Question
Consider the polynomial \(P\left( z \right) = {z^5} - 10{z^2} + 15z - 6,{\text{ }}z \in \mathbb{C}\).
The polynomial can be written in the form \(P(z) = {(z - 1)^3}({z^2} + bz + c)\).
Consider the function \(q\left( x \right) = {x^5} - 10{x^2} + 15x - 6,{\text{ }}x \in \mathbb{R}\).
Write down the sum and the product of the roots of \(P(z) = 0\).
Show that \((z - 1)\) is a factor of \(P(z)\).
Find the value of \(b\) and the value of \(c\).
Hence find the complex roots of \(P(z) = 0\).
Show that the graph of \(y = q(x)\) is concave up for \(x > 1\).
Sketch the graph of \(y = q(x)\) showing clearly any intercepts with the axes.
Markscheme
\({\text{sum}} = 0\) A1
\({\text{product}} = 6\) A1
[2 marks]
\(P(1) = 1 - 10 + 15 - 6 = 0\) M1A1
\( \Rightarrow (z - 1)\) is a factor of \(P(z)\) AG
Note: Accept use of division to show remainder is zero.
[2 marks]
METHOD 1
\({(z - 1)^3}\left( {{z^2} + bz + c} \right) = {z^5} - 10{z^2} + 15z - 6\) (M1)
by inspection \(c = 6\) A1
\(({z^3} - 3{z^2} + 3z - 1)({z^2} + bz + 6) = {z^5} - 10{z^2} + 15z - 6\) (M1)(A1)
\(b = 3\) A1
METHOD 2
\(\alpha \), \(\beta \) are two roots of the quadratic
\(b = - (\alpha + \beta ),{\text{ }}c = \alpha \beta \) (A1)
from part (a) \(1 + 1 + 1 + \alpha + \beta = 0\) (M1)
\( \Rightarrow b = 3\) A1
\(1 \times 1 \times 1 \times \alpha \beta = 6\) (M1)
\( \Rightarrow c = 6\) A1
Note: Award FT if \(b = - 7\) following through from their sum \( = 10\).
METHOD 3
\(({z^5} - 10{z^2} + 15z - 6) \div (z - 1) = {z^4} + {z^3} + {z^2} - 9z + 6\) (M1)A1
Note: This may have been seen in part (b).
\({z^4} + {z^3} + {z^2} - 9z + 6 \div (z - 1) = {z^3} + 2{z^2} + 3z - 6\) (M1)
\({z^3} + 2{z^2} + 3z - 6 \div (z - 1) = {z^2} + 3z + 6\) A1A1
[5 marks]
\({z^2} + 3z + 6 = 0\) M1
\(z = \frac{{ - 3 \pm \sqrt {9 - 4 \bullet 6} }}{2}\) M1
\( = \frac{{ - 3 \pm \sqrt { - 15} }}{2}\)
\(z = - \frac{3}{2} \pm \frac{{{\text{i}}\sqrt {15} }}{2}\) A1
(or \(z = 1\))
Notes: Award the second M1 for an attempt to use the quadratic formula or to complete the square.
Do not award FT from (c).
[3 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 20{x^3} - 20\) M1A1
for \(x > 1,{\text{ }}20{x^3} - 20 > 0 \Rightarrow \) concave up R1AG
[3 marks]
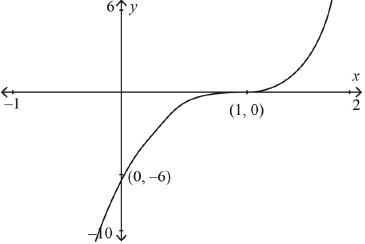
\(x\)-intercept at \((1,{\text{ }}0)\) A1
\(y\)-intercept at \((0,{\text{ }} - 6)\) A1
stationary point of inflexion at \((1,{\text{ }}0)\) with correct curvature either side A1
[3 marks]

