| Date | May 2016 | Marks available | 4 | Reference code | 16M.1.hl.TZ2.11 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 11 | Adapted from | N/A |
Question
The following graph shows the relation \(x = 3\cos 2y + 4,{\text{ }}0 \leqslant y \leqslant \pi \).
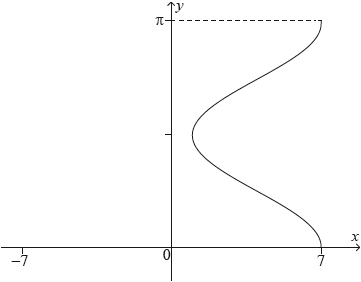
The curve is rotated 360° about the \(y\)-axis to form a volume of revolution.
A container with this shape is made with a solid base of diameter 14 cm . The container is filled with water at a rate of \({\text{2 c}}{{\text{m}}^{\text{3}}}\,{\text{mi}}{{\text{n}}^{ - 1}}\). At time \(t\) minutes, the water depth is \(h{\text{ cm, }}0 \leqslant h \leqslant \pi \) and the volume of water in the container is \(V{\text{ c}}{{\text{m}}^{\text{3}}}\).
Calculate the value of the volume generated.
(i) Given that \(\frac{{{\text{d}}V}}{{{\text{d}}h}} = \pi {(3\cos 2h + 4)^2}\), find an expression for \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\).
(ii) Find the value of \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) when \(h = \frac{\pi }{4}\).
(i) Find \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
(ii) Find the values of \(h\) for which \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}} = 0\).
(iii) By making specific reference to the shape of the container, interpret \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) at the values of \(h\) found in part (c)(ii).
Markscheme
use of \(\pi \int_a^b {{x^2}{\text{d}}y} \) (M1)
Note: Condone any or missing limits.
\(V = \pi \int_0^\pi {{{(3\cos 2y + 4)}^2}{\text{d}}y} \) (A1)
\( = \pi \int_0^\pi {(9{{\cos }^2}2y + 24\cos 2y + 16){\text{d}}y} \) A1
\(9{\cos ^2}2y = \frac{9}{2}(1 + \cos 4y)\) (M1)
\( = \pi \left[ {\frac{{9y}}{2} + \frac{9}{8}\sin 4y + 12\sin 2y + 16y} \right]_0^\pi \) M1A1
\( = \pi \left( {\frac{{9\pi }}{2} + 16\pi } \right)\) (A1)
\( = \frac{{41{\pi ^2}}}{2}{\text{ (c}}{{\text{m}}^3})\) A1
Note: If the coefficient “\(\pi \)” is absent, or eg, “\(2\pi \)” is used, only M marks are available.
[8 marks]
(i) attempting to use \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{{\text{d}}V}}{{{\text{d}}t}} \times \frac{{{\text{d}}h}}{{{\text{d}}V}}\) with \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 2\) M1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{2}{{\pi {{(3\cos 2h + 4)}^2}}}\) A1
(ii) substituting \(h = \frac{\pi }{4}\) into \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{1}{{8\pi }}{\text{ (cm}}\,{\text{mi}}{{\text{n}}^{ - 1}})\) A1
Note: Do not allow FT marks for (b)(ii).
[4 marks]
(i) \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}} = \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right) = \frac{{{\text{d}}h}}{{{\text{d}}t}} \times \frac{{\text{d}}}{{{\text{d}}h}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right)\) (M1)
\( = \frac{2}{{\pi {{(3\cos 2h + 4)}^2}}} \times \frac{{24\sin 2h}}{{\pi {{(3\cos 2h + 4)}^3}}}\) M1A1
Note: Award M1 for attempting to find \(\frac{{\text{d}}}{{{\text{d}}h}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right)\).
\( = \frac{{48\sin 2h}}{{{\pi ^2}{{(3\cos 2h + 4)}^5}}}\) A1
(ii) \(\sin 2h = 0 \Rightarrow h = 0,{\text{ }}\frac{\pi }{2},{\text{ }}\pi \) A1
Note: Award A1 for \(\sin 2h = 0 \Rightarrow h = 0,{\text{ }}\frac{\pi }{2},{\text{ }}\pi \) from an incorrect \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
(iii) METHOD 1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) is a minimum at \(h = 0,{\text{ }}\pi \) and the container is widest at these values R1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) is a maximum at \(h = \frac{\pi }{2}\) and the container is narrowest at this value R1
[7 marks]
Examiners report
Part (a) was often answered well, though for some reason a minority tended to use the incorrect \(\pi \int {{{(3\cos 2y)}^2}{\text{d}}y} \) and gained few marks thereafter. Incorrect limits were sometimes seen, which led to only method marks being available. A pleasing number were able to deal with the integration of \({\cos ^2}2y\) through the use of the correct identity.
Part (b) was well answered and did not pose too many problems.
Correct answers to part (c) were rarely seen. Only the very best candidates appreciated the correct use of the chain rule when trying to determine an expression for \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).

