| Date | May 2014 | Marks available | 3 | Reference code | 14M.1.hl.TZ2.13 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 13 | Adapted from | N/A |
Question
The graph of the function \(f(x) = \frac{{x + 1}}{{{x^2} + 1}}\) is shown below.
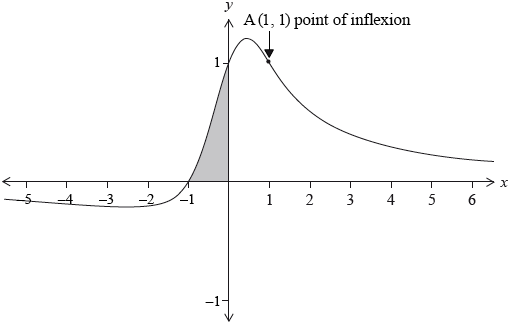
The point (1, 1) is a point of inflexion. There are two other points of inflexion.
Find \(f'(x)\).
Hence find the \(x\)-coordinates of the points where the gradient of the graph of \(f\) is zero.
Find \(f''(x)\) expressing your answer in the form \(\frac{{p(x)}}{{{{({x^2} + 1)}^3}}}\), where \(p(x)\) is a polynomial of degree 3.
Find the \(x\)-coordinates of the other two points of inflexion.
Find the area of the shaded region. Express your answer in the form \(\frac{\pi }{a} - \ln \sqrt b \), where \(a\) and \(b\) are integers.
Markscheme
(a) \(f'(x) = \frac{{\left( {{x^2} + 1} \right) - 2x(x + 1)}}{{{{\left( {{x^2} + 1} \right)}^2}}}{\text{ }}\left( { = \frac{{ - {x^2} - 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}} \right)\) M1A1
[2 marks]
\(\frac{{ - {x^2} - 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0\)
\(x = - 1 \pm \sqrt 2 \) A1
[1 mark]
\(f''(x) = \frac{{( - 2x - 2){{\left( {{x^2} + 1} \right)}^2} - 2(2x)\left( {{x^2} + 1} \right)\left( { - {x^2} - 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^4}}}\) A1A1
Note: Award A1 for \(( - 2x - 2){\left( {{x^2} + 1} \right)^2}\) or equivalent.
Note: Award A1 for \( - 2(2x)\left( {{x^2} + 1} \right)\left( { - {x^2} - 2x + 1} \right)\) or equivalent.
\( = \frac{{( - 2x - 2)\left( {{x^2} + 1} \right) - 4x\left( { - {x^2} - 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}\)
\( = \frac{{2{x^3} + 6{x^2} - 6x - 2}}{{{{\left( {{x^2} + 1} \right)}^3}}}\) A1
\(\left( { = \frac{{2\left( {{x^3} + 3{x^2} - 3x - 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}} \right)\)
[3 marks]
recognition that \((x - 1)\) is a factor (R1)
\((x - 1)\left( {{x^2} + bx + c} \right) = \left( {{x^3} + 3{x^2} - 3x - 1} \right)\) M1
\( \Rightarrow {x^2} + 4x + 1 = 0\) A1
\(x = - 2 \pm \sqrt 3 \) A1
Note: Allow long division / synthetic division.
[4 marks]
\(\int_{ - 1}^0 {\frac{{x + 1}}{{{x^2} + 1}}{\text{d}}x} \) M1
\(\int {\frac{{x + 1}}{{{x^2} + 1}}{\text{d}}x = \int {\frac{x}{{{x^2} + 1}}{\text{d}}x + \int {\frac{1}{{{x^2} + 1}}{\text{d}}x} } } \) M1
\( = \frac{1}{2}\ln \left( {{x^2} + 1} \right) + \arctan (x)\) A1A1
\( = \left[ {\frac{1}{2}\ln \left( {{x^2} + 1} \right) + \arctan (x)} \right]_{ - 1}^0 = \frac{1}{2}\ln 1 + \arctan 0 - \frac{1}{2}\ln 2 - \arctan ( - 1)\) M1
\( = \frac{\pi }{4} - \ln \sqrt 2 \) A1
[6 marks]

