| Date | May 2016 | Marks available | 4 | Reference code | 16M.2.hl.TZ1.11 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 11 | Adapted from | N/A |
Question
Let \(f(x) = {x^4} + 0.2{x^3} - 5.8{x^2} - x + 4,{\text{ }}x \in \mathbb{R}\).
The domain of \(f\) is now restricted to \([0,{\text{ }}a]\).
Let \(g(x) = 2\sin (x - 1) - 3,{\text{ }} - \frac{\pi }{2} + 1 \leqslant x \leqslant \frac{\pi }{2} + 1\).
Find the solutions of \(f(x) > 0\).
For the curve \(y = f(x)\).
(i) Find the coordinates of both local minimum points.
(ii) Find the \(x\)-coordinates of the points of inflexion.
Write down the largest value of \(a\) for which \(f\) has an inverse. Give your answer correct to 3 significant figures.
For this value of a sketch the graphs of \(y = f(x)\) and \(y = {f^{ - 1}}(x)\) on the same set of axes, showing clearly the coordinates of the end points of each curve.
Solve \({f^{ - 1}}(x) = 1\).
Find an expression for \({g^{ - 1}}(x)\), stating the domain.
Solve \(({f^{ - 1}} \circ g)(x) < 1\).
Markscheme
valid method eg, sketch of curve or critical values found (M1)
\(x < - 2.24,{\text{ }}x > 2.24,\) A1
\( - 1 < x < 0.8\) A1
Note: Award M1A1A0 for correct intervals but with inclusive inequalities.
[3 marks]
(i) \((1.67,{\text{ }} - 5.14),{\text{ }}( - 1.74,{\text{ }} - 3.71)\) A1A1
Note: Award A1A0 for any two correct terms.
(ii) \(f'(x) = 4{x^3} + 0.6{x^2} - 11.6x - 1\)
\(f''(x) = 12{x^2} + 1.2x - 11.6 = 0\) (M1)
\( - 1.03,{\text{ }}0.934\) A1A1
Note: M1 should be awarded if graphical method to find zeros of \(f''(x)\) or turning points of \(f'(x)\) is shown.
[5 marks]
1.67 A1
[2 marks]
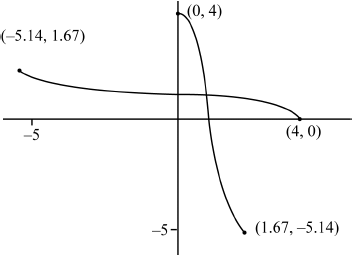 M1A1A1
M1A1A1
Note: Award M1 for reflection of their \(y = f(x)\) in the line \(y = x\) provided their \(f\) is one-one.
A1 for \((0,{\text{ }}4)\), \((4,{\text{ }}0)\) (Accept axis intercept values) A1 for the other two sets of coordinates of other end points
[2 marks]
\(x = f(1)\) M1
\( = - 1.6\) A1
[2 marks]
\(y = 2\sin (x - 1) - 3\)
\(x = 2\sin (y - 1) - 3\) (M1)
\(\left( {{g^{ - 1}}(x) = } \right){\text{ }}\arcsin \left( {\frac{{x + 3}}{2}} \right) + 1\) A1
\( - 5 \leqslant x \leqslant - 1\) A1A1
Note: Award A1 for −5 and −1, and A1 for correct inequalities if numbers are reasonable.
[8 marks]
\({f^{ - 1}}\left( {g(x)} \right) < 1\)
\(g(x) > - 1.6\) (M1)
\(x > {g^{ - 1}}( - 1.6) = 1.78\) (A1)
Note: Accept = in the above.
\(1.78 < x \leqslant \frac{\pi }{2} + 1\) A1A1
Note: A1 for \(x > 1.78\) (allow ≥) and A1 for \(x \leqslant \frac{\pi }{2} + 1\).
[4 marks]
Examiners report
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Part d(i) was generally well done, but there were few correct answers for d(ii).
Part d(i) was generally well done, but there were few correct answers for d(ii).

