| Date | May 2015 | Marks available | 4 | Reference code | 15M.1.hl.TZ2.10 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
The function \(f\) is defined by \(f(x) = \frac{{3x}}{{x - 2}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne 2\).
Sketch the graph of \(y = f(x)\), indicating clearly any asymptotes and points of intersection with the \(x\) and \(y\) axes.
Find an expression for \({f^{ - 1}}(x)\).
Find all values of \(x\) for which \(f(x) = {f^{ - 1}}(x)\).
Solve the inequality \(\left| {f(x)} \right| < \frac{3}{2}\).
Solve the inequality \(f\left( {\left| x \right|} \right) < \frac{3}{2}\).
Markscheme
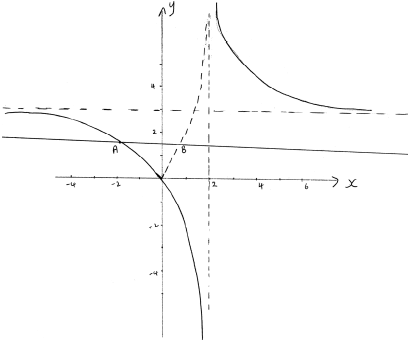
Note: In the diagram, points marked \(A\) and \(B\) refer to part (d) and do not need to be seen in part (a).
shape of curve A1
Note: This mark can only be awarded if there appear to be both horizontal and vertical asymptotes.
intersection at \((0,{\text{ }}0)\) A1
horizontal asymptote at \(y = 3\) A1
vertical asymptote at \(x = 2\) A1
[4 marks]
\(y = \frac{{3x}}{{x - 2}}\)
\(xy - 2y = 3x\) M1A1
\(xy - 3x = 2y\)
\(x = \frac{{2y}}{{y - 3}}\)
\(\left( {{f^{ - 1}}(x)} \right) = \frac{{2x}}{{x - 3}}\) M1A1
Note: Final M1 is for interchanging of \(x\) and \(y\), which may be seen at any stage.
[4 marks]
METHOD 1
attempt to solve \(\frac{{2x}}{{x - 3}} = \frac{{3x}}{{x - 2}}\) (M1)
\(2x(x - 2) = 3x(x - 3)\)
\(x\left[ {2(x - 2) - 3(x - 3)} \right] = 0\)
\(x(5 - x) = 0\)
\(x = 0\;\;\;\)or\(\;\;\;x = 5\) A1A1
METHOD 2
\(x = \frac{{3x}}{{x - 2}}\;\;\;\)or\(\;\;\;x = \frac{{2x}}{{x - 3}}\) (M1)
\(x = 0\;\;\;\)or\(\;\;\;x = 5\) A1A1
[3 marks]
METHOD 1
at \({\text{A}}:\frac{{3x}}{{x - 2}} = \frac{3}{2}\) AND at \({\text{B}}:\frac{{3x}}{{x - 2}} = - \frac{3}{2}\) M1
\(6x = 3x - 6\)
\(x = - 2\) A1
\(6x = 6 - 3x\)
\(x = \frac{2}{3}\) A1
solution is \( - 2 < x < \frac{2}{3}\) A1
METHOD 2
\({\left( {\frac{{3x}}{{x - 2}}} \right)^2} < {\left( {\frac{3}{2}} \right)^2}\) M1
\(9{x^2} < \frac{9}{4}{(x - 2)^2}\)
\(3{x^2} + 4x - 4 < 0\)
\((3x - 2)(x + 2) < 0\)
\(x = - 2\) (A1)
\(x = \frac{2}{3}\) (A1)
solution is \( - 2 < x < \frac{2}{3}\) A1
[4 marks]
\( - 2 < x < 2\) A1A1
Note: A1 for correct end points, A1 for correct inequalities.
Note: If working is shown, then A marks may only be awarded following correct working.
[2 marks]
Total [17 marks]

