| Date | November 2015 | Marks available | 6 | Reference code | 15N.2.hl.TZ0.12 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Explain, Sketch, and State | Question number | 12 | Adapted from | N/A |
Question
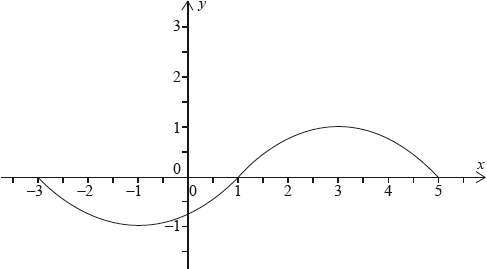
The following graph represents a function \(y = f(x)\), where \( - 3 \le x \le 5\).
The function has a maximum at \((3,{\text{ }}1)\) and a minimum at \(( - 1,{\text{ }} - 1)\).
The functions \(u\) and \(v\) are defined as \(u(x) = x - 3,{\text{ }}v(x) = 2x\) where \(x \in \mathbb{R}\).
(i) State the range of the function \(u \circ f\).
(ii) State the range of the function \(u \circ v \circ f\).
(iii) Find the largest possible domain of the function \(f \circ v \circ u\).
(i) Explain why \(f\) does not have an inverse.
(ii) The domain of \(f\) is restricted to define a function \(g\) so that it has an inverse \({g^{ - 1}}\).
State the largest possible domain of \(g\).
(iii) Sketch a graph of \(y = {g^{ - 1}}(x)\), showing clearly the \(y\)-intercept and stating the coordinates of the endpoints.
Consider the function defined by \(h(x) = \frac{{2x - 5}}{{x + d}}\), \(x \ne - d\) and \(d \in \mathbb{R}\).
(i) Find an expression for the inverse function \({h^{ - 1}}(x)\).
(ii) Find the value of \(d\) such that \(h\) is a self-inverse function.
For this value of \(d\), there is a function \(k\) such that \(h \circ k(x) = \frac{{2x}}{{x + 1}},{\text{ }}x \ne - 1\).
(iii) Find \(k(x)\).
Markscheme
Note: For Q12(a) (i) – (iii) and (b) (ii), award A1 for correct endpoints and, if correct, award A1 for a closed interval.
Further, award A1A0 for one correct endpoint and a closed interval.
(i) \( - 4 \le y \le - 2\) A1A1
(ii) \( - 5 \le y \le - 1\) A1A1
(iii) \( - 3 \le 2x - 6 \le 5\) (M1)
Note: Award M1 for \(f(2x - 6)\).
\(3 \le 2x \le 11\)
\(\frac{3}{2} \le x \le \frac{{11}}{2}\) A1A1
[7 marks]
(i) any valid argument eg \(f\) is not one to one, \(f\) is many to one, fails horizontal line test, not injective R1
(ii) largest domain for the function \(g(x)\) to have an inverse is \([ - 1,{\text{ }}3]\) A1A1
(iii) 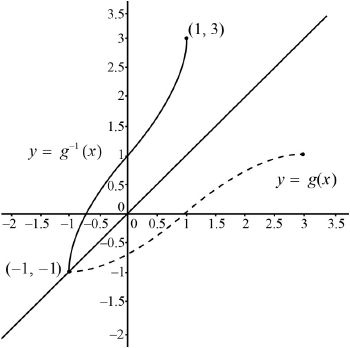
\(y\)-intercept indicated (coordinates not required) A1
correct shape A1
coordinates of end points \((1,{\text{ }}3)\) and \(( - 1,{\text{ }} - 1)\) A1
Note: Do not award any of the above marks for a graph that is not one to one.
[6 marks]
(i) \(y = \frac{{2x - 5}}{{x + d}}\)
\((x + d)y = 2x - 5\) M1
Note: Award M1 for attempting to rearrange \(x\) and \(y\) in a linear expression.
\(x(y - 2) = - dy - 5\) (A1)
\(x = \frac{{ - dy - 5}}{{y - 2}}\) (A1)
Note: \(x\) and \(y\) can be interchanged at any stage
\({h^{ - 1}}(x) = \frac{{ - dx - 5}}{{x - 2}}\) A1
Note: Award A1 only if \({h^{ - 1}}(x)\) is seen.
(ii) self Inverse \( \Rightarrow h(x) = {h^{ - 1}}(x)\)
\(\frac{{2x - 5}}{{x + d}} \equiv \frac{{ - dx - 5}}{{x - 2}}\) (M1)
\(d = - 2\) A1
(iii) METHOD 1
\(\frac{{2k(x) - 5}}{{k(x) - 2}} = \frac{{2x}}{{x + 1}}\) (M1)
\(k(x) = \frac{{x + 5}}{2}\) A1
METHOD 2
\({h^{ - 1}}\left( {\frac{{2x}}{{x + 1}}} \right) = \frac{{2\left( {\frac{{2x}}{{x + 1}}} \right) - 5}}{{\frac{{2x}}{{x + 1}} - 2}}\) (M1)
\(k(x) = \frac{{x + 5}}{2}\) A1
[8 marks]
Total [21 marks]

