| Date | May 2017 | Marks available | 3 | Reference code | 17M.2.sl.TZ1.4 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Calculate | Question number | 4 | Adapted from | N/A |
Question
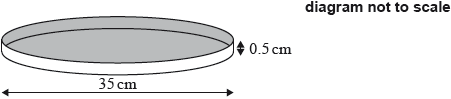
A pan, in which to cook a pizza, is in the shape of a cylinder. The pan has a diameter of 35 cm and a height of 0.5 cm.
A chef had enough pizza dough to exactly fill the pan. The dough was in the shape of a sphere.
The pizza was cooked in a hot oven. Once taken out of the oven, the pizza was placed in a dining room.
The temperature, \(P\), of the pizza, in degrees Celsius, °C, can be modelled by
\[P(t) = a{(2.06)^{ - t}} + 19,{\text{ }}t \geqslant 0\]
where \(a\) is a constant and \(t\) is the time, in minutes, since the pizza was taken out of the oven.
When the pizza was taken out of the oven its temperature was 230 °C.
The pizza can be eaten once its temperature drops to 45 °C.
Calculate the volume of this pan.
Find the radius of the sphere in cm, correct to one decimal place.
Find the value of \(a\).
Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.
Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.
In the context of this model, state what the value of 19 represents.
Markscheme
\((V = ){\text{ }}\pi \times {{\text{(17.5)}}^2} \times 0.5\) (A1)(M1)
Notes: Award (A1) for 17.5 (or equivalent) seen.
Award (M1) for correct substitutions into volume of a cylinder formula.
\( = 481{\text{ c}}{{\text{m}}^3}{\text{ }}(481.056 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}153.125\pi {\text{ c}}{{\text{m}}^3})\) (A1)(G2)
[3 marks]
\(\frac{4}{3} \times \pi \times {r^3} = 481.056 \ldots \) (M1)
Note: Award (M1) for equating their answer to part (a) to the volume of sphere.
\({r^3} = \frac{{3 \times 481.056 \ldots }}{{4\pi }}{\text{ }}( = 114.843 \ldots )\) (M1)
Note: Award (M1) for correctly rearranging so \({r^3}\) is the subject.
\(r = 4.86074 \ldots {\text{ (cm)}}\) (A1)(ft)(G2)
Note: Award (A1) for correct unrounded answer seen. Follow through from part (a).
\( = 4.9{\text{ (cm)}}\) (A1)(ft)(G3)
Note: The final (A1)(ft) is awarded for rounding their unrounded answer to one decimal place.
[4 marks]
\(230 = a{(2.06)^0} + 19\) (M1)
Note: Award (M1) for correct substitution.
\(a = 211\) (A1)(G2)
[2 marks]
\((P = ){\text{ }}211 \times {(2.06)^{ - 5}} + 19\) (M1)
Note: Award (M1) for correct substitution into the function, \(P(t)\). Follow through from part (c). The negative sign in the exponent is required for correct substitution.
\( = 24.7\) (°C) \((24.6878 \ldots \) (°C)) (A1)(ft)(G2)
[2 marks]
\(45 = 211 \times {(2.06)^{ - t}} + 19\) (M1)
Note: Award (M1) for equating 45 to the exponential equation and for correct substitution (follow through for their \(a\) in part (c)).
\((t = ){\text{ }}2.89711 \ldots \) (A1)(ft)(G1)
\(174{\text{ (seconds) }}\left( {173.826 \ldots {\text{ (seconds)}}} \right)\) (A1)(ft)(G2)
Note: Award final (A1)(ft) for converting their \({\text{2.89711}} \ldots \) minutes into seconds.
[3 marks]
the temperature of the (dining) room (A1)
OR
the lowest final temperature to which the pizza will cool (A1)
[1 mark]

