| Date | May 2014 | Marks available | 2 | Reference code | 14M.1.sl.TZ2.11 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Calculate | Question number | 11 | Adapted from | N/A |
Question
In a trial for a new drug, scientists found that the amount of the drug in the bloodstream decreased over time, according to the model
\[D(t) = 1.2 \times {(0.87)^t},{\text{ }}t \geqslant 0\]
where \(D\) is the amount of the drug in the bloodstream in mg per litre \({\text{(mg}}\,{{\text{l}}^{ - 1}}{\text{)}}\) and \(t\) is the time in hours.
Write down the amount of the drug in the bloodstream at \(t = 0\).
Calculate the amount of the drug in the bloodstream after 3 hours.
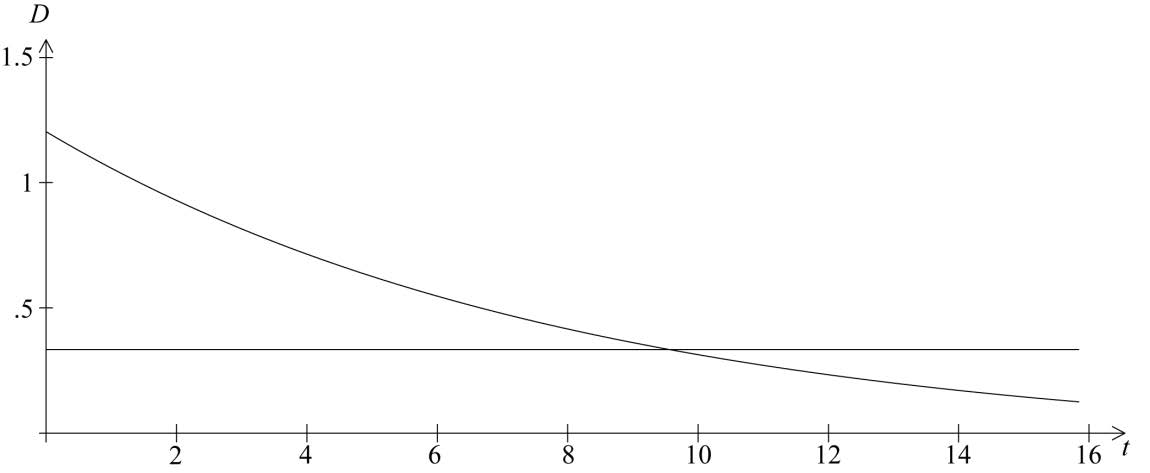
Use your graphic display calculator to determine the time it takes for the amount of the drug in the bloodstream to decrease to \(0.333{\text{ mg}}{{\text{1}}^{ - 1}}\).
Markscheme
\(1.2{\text{ (mg}}\,{{\text{l}}^{ - 1}}{\text{)}}\) (A1) (C1)
[1 mark]
\(1.2 \times {(0.87)^3}\) (M1)
Note: Award (M1) for correct substitution into given formula.
\( = {\text{0.790 (mg}}\,{{\text{l}}^{ - 1}}{\text{) (0.790203}} \ldots {\text{)}}\) (A1) (C2)
[2 marks]
\(1.2 \times {0.87^t} = 0.333\) (M1)
Note: Award (M1) for setting up the equation.
 (M1)
(M1)
Notes: Some indication of scale is to be shown, for example the window used on the calculator.
Accept alternative methods.
\(9.21\) (hours) (\(9.20519…\), 9 hours 12 minutes, 9:12) (A1) (C3)
[3 marks]

