| Date | November 2016 | Marks available | 2 | Reference code | 16N.1.sl.TZ0.15 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Write down | Question number | 15 | Adapted from | N/A |
Question
Gabriella purchases a new car.
The car’s value in dollars, \(V\), is modelled by the function
\[V(t) = 12870 - k{(1.1)^t},{\text{ }}t \geqslant 0\]
where \(t\) is the number of years since the car was purchased and \(k\) is a constant.
After two years, the car’s value is $9143.20.
This model is defined for \(0 \leqslant t \leqslant n\). At \(n\) years the car’s value will be zero dollars.
Write down, and simplify, an expression for the car’s value when Gabriella purchased it.
Find the value of \(k\).
Find the value of \(n\).
Markscheme
\(12870 - k{(1.1)^0}\) (M1)
Note: Award (M1) for correct substitution into \(V(t)\).
\( = 12870 - k\) (A1) (C2)
Note: Accept \(12870 - 3080\) OR 9790 for a final answer.
[2 marks]
\(9143.20 = 12870 - k{(1.1)^2}\) (M1)
Note: Award (M1) for correct substitution into \(V(t)\).
\((k = ){\text{ }}3080\) (A1) (C2)
[2 marks]
\(12870 - 3080{(1.1)^n} = 0\) (M1)
Note: Award (M1) for correct substitution into \(V(t)\).
OR
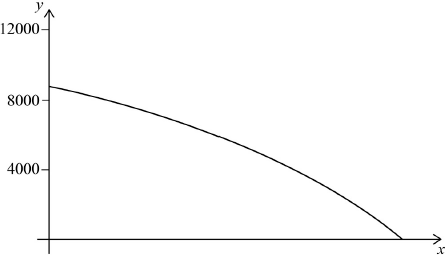 (M1)
(M1)
Note: Award (M1) for a correctly shaped curve with some indication of scale on the vertical axis.
\((n = ){\text{ }}15.0{\text{ }}(15.0033 \ldots )\) (A1)(ft) (C2)
Note: Follow through from part (b).
[2 marks]

