| Date | May 2014 | Marks available | 3 | Reference code | 14M.1.sl.TZ1.11 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 11 | Adapted from | N/A |
Question
The amount of electrical charge, C, stored in a mobile phone battery is modelled by \(C(t) = 2.5 - {2^{ - t}}\), where t, in hours, is the time for which the battery is being charged.
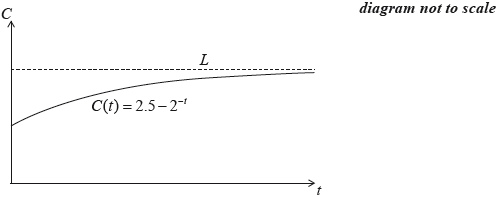
Write down the amount of electrical charge in the battery at \(t = 0\).
The line \(L\) is the horizontal asymptote to the graph.
Write down the equation of \(L\).
To download a game to the mobile phone, an electrical charge of 2.4 units is needed.
Find the time taken to reach this charge. Give your answer correct to the nearest minute.
Markscheme
\(1.5\) (A1) (C1)
[1 mark]
\(C = 2.5\) (accept \(y = 2.5\)) (A1)(A1) (C2)
Notes: Award (A1) for \(C{\text{ (or }}y) = \) a positive constant, (A1) for the constant \(= 2.5\).
Answer must be an equation.
[2 marks]
\(2.4 = 2.5 - {2^{ - t}}\) (M1)
Note: Award (M1) for setting the equation equal to 2.4 or for a horizontal line drawn at approximately \(C = 2.4\).
Allow \(x\) instead of \(t\).
OR
\( - t\ln (2) = \ln (0.1)\) (M1)
\(t = 3.32192 \ldots \) (A1)
\(t = 3{\text{ hours and 19 minutes (199 minutes)}}\) (A1)(ft) (C3)
Note: Award the final (A1)(ft) for correct conversion of their time in hours to the nearest minute.
[3 marks]

