| Date | November 2017 | Marks available | 1 | Reference code | 17N.1.sl.TZ0.12 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Write down | Question number | 12 | Adapted from | N/A |
Question
Sejah placed a baking tin, that contained cake mix, in a preheated oven in order to bake a cake. The temperature in the centre of the cake mix, \(T\), in degrees Celsius (°C) is given by
\[T(t) = 150 - a \times {(1.1)^{ - t}}\]
where \(t\) is the time, in minutes, since the baking tin was placed in the oven. The graph of \(T\) is shown in the following diagram.
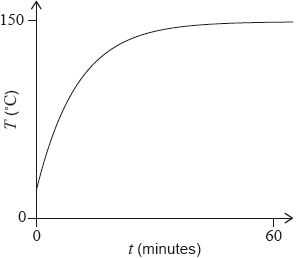
The temperature in the centre of the cake mix was 18 °C when placed in the oven.
The baking tin is removed from the oven 15 minutes after the temperature in the centre of the cake mix has reached 130 °C.
Write down what the value of 150 represents in the context of the question.
Find the value of \(a\).
Find the total time that the baking tin is in the oven.
Markscheme
the temperature in the oven (A1)
OR
the maximum possible temperature of the cake mix (A1) (C1)
Note: Award (A0) for “the maximum temperature”.
[1 mark]
\(18 = 150 - a( \times 1.1^\circ )\) (M1)
Note: Award (M1) for correct substitution of 18 and 0. Substitution of 0 can be implied.
\((a) = 132\) (A1) (C2)
[2 marks]
\(150-132 \times {1.1^{ - t}} = 130\) (M1)
Note: Award (M1) for substituting their a and equating to 130. Accept an inequality.
Award (M1) for a sketch of the horizontal line on the graph.
\(t = 19.8{\text{ }}(19.7992 \ldots )\) (A1)(ft)
Note: Follow through from part (b).
34.8 (minutes) (34.7992…, 34 minutes 48 seconds) (A1)(ft) (C3)
Note: Award the final (A1) for adding 15 minutes to their \(t\) value.
In part (c), award (C2) for a final answer of 19.8 with no working.
[3 marks]

