| Date | May 2015 | Marks available | 2 | Reference code | 15M.2.sl.TZ1.6 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
A cup of boiling water is placed in a room to cool. The temperature of the room is 20°C . This situation can be modelled by the exponential function \(T = a + b({k^{ - m}})\), where \(T\) is the temperature of the water, in °C , and \(m\) is the number of minutes for which the cup has been placed in the room. A sketch of the situation is given as follows.
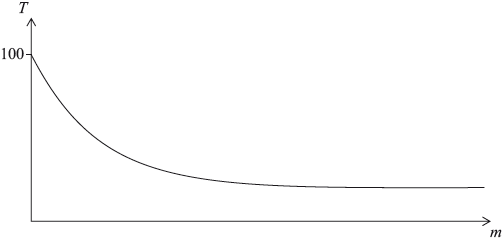
Explain why \(a = 20\).
Initially, at \(m = 0\), the temperature of the water is 100°C.
Find the value of \(b\).
After being placed in the room for one minute, the temperature of the water is 84°C.
Show that \(k = 1.25\).
After being placed in the room for one minute, the temperature of the water is 84°C.
Find the temperature of the water three minutes after it has been placed in the room.
After being placed in the room for one minute, the temperature of the water is 84°C.
Find the total time needed for the water to reach a temperature of 35°C. Give your answer in minutes and seconds, correct to the nearest second.
Markscheme
the temperature of the water cannot fall below room temperature (R1)
an (informal) explanation that as \(m \to \infty ,{\text{ }}{k^{ - m}} \to 0\) R1)
OR
recognition that there is a horizontal asymptote at \(y = a\) (R1)
Note: Award (R1) for a contextual reason involving room temperature.
Award (R1) for a mathematical reason similar to one of the two alternatives.
\(100 = 20 + b({k^0})\) (M1)
Note: Award (M1) for substituting \(100\), \(20\) and \(0\).
\(b = 80\) (A1)(G2)
Note: The (A1) is awarded only if all working seen is consistent with the final answer of \(80\).
\(84 = 20 + 80{k^{ - 1}}\) (M1)
Note: Substituting \(k = 1.25\) at any stage is an invalid method and is awarded (M0)(M0). Award (M1) for correctly substituting \(84\), \(20\) and their \(80\).
\(\frac{{64}}{{80}} = {k^{ - 1}}\) (M1)
\(k = 1.25\) (AG)
Note: Award (M1) for correct rearrangement that isolates \(k\); \(k = 1.25\) must be consistent with their working and the conclusion \(k = 1.25\) must be seen.
\(T = 20 + 80({1.25^{ - 3}})\) (M1)
Note: Award (M1) for their correct substitutions into \(T\). Follow through from part (b) and \(k = 1.25\).
\(T = 61.0\;\;\;(60.96)\) (A1)(ft)(G2)
\(35 = 20 + 80({1.25^{ - m}})\) (M1)
Note: Award (M1) for their correct substitutions into \(T\). Follow through from part (b). Accept graphical solutions. Award (M1) for sketch of function.
\((m = ){\text{ }}7.50{\text{ (minutes)}}\;\;\;{\text{(7.50179}} \ldots {\text{)}}\) (A1)(ft)(G2)
7 minutes and 30 seconds (A1)
Note: Award the final (A1) for correct conversion of their \(m\) in minutes to minutes and seconds, but only if answer in minutes is explicitly shown.
Examiners report
Comments on some of the G2 forms indicated that teachers felt the presence of three parameters in the formula was inconsistent with the aims of Mathematical Studies; however, one parameter was given and a justification required, a second required knowledge only of k0=1 and the third was also given. Candidates should have been exposed to graphs of this type in their classwork.
The response of the candidature indicated that most were able to make some progress with the question, though for many the “show that” part was not attempted. As in previous sessions, comments were made about the use (or not) of logarithms in the final part – logarithms are not part of the Mathematical Studies SL syllabus (however, their correct use is never penalized), but efficient use of the GDC is very much part of a candidate’s “toolbox”. Questions of this nature – essentially requiring the use of the GDC as part of a problem solving exercise – will continue to be set.
Comments on some of the G2 forms indicated that teachers felt the presence of three parameters in the formula was inconsistent with the aims of Mathematical Studies; however, one parameter was given and a justification required, a second required knowledge only of k0=1 and the third was also given. Candidates should have been exposed to graphs of this type in their classwork.
The response of the candidature indicated that most were able to make some progress with the question, though for many the “show that” part was not attempted. As in previous sessions, comments were made about the use (or not) of logarithms in the final part – logarithms are not part of the Mathematical Studies SL syllabus (however, their correct use is never penalized), but efficient use of the GDC is very much part of a candidate’s “toolbox”. Questions of this nature – essentially requiring the use of the GDC as part of a problem solving exercise – will continue to be set.
Comments on some of the G2 forms indicated that teachers felt the presence of three parameters in the formula was inconsistent with the aims of Mathematical Studies; however, one parameter was given and a justification required, a second required knowledge only of k0=1 and the third was also given. Candidates should have been exposed to graphs of this type in their classwork.
The response of the candidature indicated that most were able to make some progress with the question, though for many the “show that” part was not attempted. As in previous sessions, comments were made about the use (or not) of logarithms in the final part – logarithms are not part of the Mathematical Studies SL syllabus (however, their correct use is never penalized), but efficient use of the GDC is very much part of a candidate’s “toolbox”. Questions of this nature – essentially requiring the use of the GDC as part of a problem solving exercise – will continue to be set.
Comments on some of the G2 forms indicated that teachers felt the presence of three parameters in the formula was inconsistent with the aims of Mathematical Studies; however, one parameter was given and a justification required, a second required knowledge only of k0=1 and the third was also given. Candidates should have been exposed to graphs of this type in their classwork.
The response of the candidature indicated that most were able to make some progress with the question, though for many the “show that” part was not attempted. As in previous sessions, comments were made about the use (or not) of logarithms in the final part – logarithms are not part of the Mathematical Studies SL syllabus (however, their correct use is never penalized), but efficient use of the GDC is very much part of a candidate’s “toolbox”. Questions of this nature – essentially requiring the use of the GDC as part of a problem solving exercise – will continue to be set.
Comments on some of the G2 forms indicated that teachers felt the presence of three parameters in the formula was inconsistent with the aims of Mathematical Studies; however, one parameter was given and a justification required, a second required knowledge only of k0=1 and the third was also given. Candidates should have been exposed to graphs of this type in their classwork.
The response of the candidature indicated that most were able to make some progress with the question, though for many the “show that” part was not attempted. As in previous sessions, comments were made about the use (or not) of logarithms in the final part – logarithms are not part of the Mathematical Studies SL syllabus (however, their correct use is never penalized), but efficient use of the GDC is very much part of a candidate’s “toolbox”. Questions of this nature – essentially requiring the use of the GDC as part of a problem solving exercise – will continue to be set.

