| Date | May 2017 | Marks available | 4 | Reference code | 17M.2.sl.TZ1.3 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Sketch | Question number | 3 | Adapted from | N/A |
Question
Consider the function \(f(x) = 0.3{x^3} + \frac{{10}}{x} + {2^{ - x}}\).
Consider a second function, \(g(x) = 2x - 3\).
Calculate \(f(1)\).
Sketch the graph of \(y = f(x)\) for \( - 7 \leqslant x \leqslant 4\) and \( - 30 \leqslant y \leqslant 30\).
Write down the equation of the vertical asymptote.
Write down the coordinates of the \(x\)-intercept.
Write down the possible values of \(x\) for which \(x < 0\) and \(f’(x) > 0\).
Find the solution of \(f(x) = g(x)\).
Markscheme
\(0.3{(1)^3} + \frac{{10}}{1} + {2^{ - 1}}\) (M1)
Note: Award (M1) for correct substitution into function.
\( = 10.8\) (A1)(G2)
[2 marks]
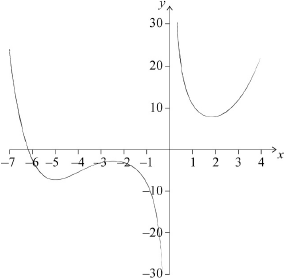 (A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)
Note: Award (A1) for indication of correct window and labelled axes.
Award (A1) for correct shape and position for \(x < 0\) (with the local maximum, local minimum and \(x\)-intercept in relative approximate location in \({{\text{3}}^{{\text{rd}}}}\) quadrant).
Award (A1) for correct shape and position for \(x > 0\) (with the local minimum in relative approximate location in \({{\text{1}}^{{\text{st}}}}\) quadrant).
Award (A1) for smooth curve with indication of asymptote (graph should not touch \(y\)-axis and should not curve away from the \(y\)-axis). The asymptote is only assessed in this mark.
[4 marks]
\(x = 0\) (A2)
Note: Award (A1) for “\(x = {\text{(a constant)}}\)” and (A1) for “\({\text{(a constant)}} = 0\)”.
The answer must be an equation.
[2 marks]
\(( - 6.18,{\text{ }}0){\text{ }}( - 6.17516 \ldots ,{\text{ }}0)\) (A1)(A1)
Note: Award (A1) for each correct coordinate. Award (A0)(A1) if parentheses are missing.
[2 marks]
\( - 4.99 < x < - 2.47{\text{ }}( - 4.98688 \ldots < x < - 2.46635 \ldots )\) (A1)(A1)
Note: Award (A1) for both correct end points, (A1) for strict inequalities used with 2 endpoints.
[2 marks]
\(0.3{x^3} + \frac{{10}}{x} + {2^{ - x}} = 2x - 3\) (M1)
Note: Award (M1) for equating the expressions for \(f\) and \(g\) or for the line \(y = 2x - 3\) sketched (positive gradient, negative \(y\)-intercept) on their graph from part (a).
\((x = ){\text{ }} - 1.34{\text{ }}( - 1.33650 \ldots )\) (A1)(G2)
Note: Award a maximum of (M1)(A0) or (G1) for coordinate pair seen as final answer.
[2 marks]

