| Date | May 2011 | Marks available | 2 | Reference code | 11M.2.sl.TZ2.6 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
Let the random variable X be normally distributed with mean 25, as shown in the following diagram.
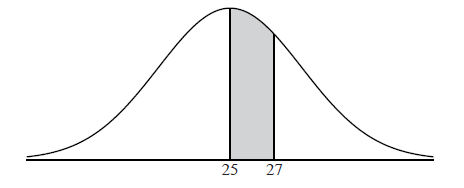
The shaded region between 25 and 27 represents \(30\% \) of the distribution.
Find \({\rm{P}}(X > 27)\) .
Find the standard deviation of X .
Markscheme
symmetry of normal curve (M1)
e.g. \({\rm{P}}(X < 25) = 0.5\)
\({\rm{P}}(X > 27) = 0.2\) A1 N2
[2 marks]
METHOD 1
finding standardized value (A1)
e.g. \(\frac{{27 - 25}}{\sigma }\)
evidence of complement (M1)
e.g. \(1 - p\) , \({\rm{P}}(X < 27)\) , 0.8
finding z-score (A1)
e.g. \(z = 0.84 \ldots \)
attempt to set up equation involving the standardized value M1
e.g. \(0.84 = \frac{{27 - 25}}{\sigma }\) , \(0.84 = \frac{{X - \mu }}{\sigma }\)
\(\sigma = 2.38\) A1 N3
METHOD 2
set up using normal CDF function and probability (M1)
e.g. \({\rm{P}}(25 < X < 27) = 0.3\) , \({\rm{P}}(X < 27) = 0.8\)
correct equation A2
e.g. \({\rm{P}}(25 < X < 27) = 0.3\) , \({\rm{P}}(X > 27) = 0.2\)
attempt to solve the equation using GDC (M1)
e.g. solver, graph, trial and error (more than two trials must be shown)
\(\sigma = 2.38\) A1 N3
[5 marks]
Examiners report
This question proved challenging for many candidates. A surprising number did not use the symmetry of the normal curve to find the probability required in (a). While many students were able to set up a standardized equation in (b), far fewer were able to use the complement to find the correct z-score. Others used 0.8 as the z-score. A common confusion when approaching parts (a) and (b) was whether to use a probability or a z-score. Additionally, many candidates seemed unsure of appropriate notation on this problem which would have allowed them to better demonstrate their method.
This question proved challenging for many candidates. A surprising number did not use the symmetry of the normal curve to find the probability required in (a). While many students were able to set up a standardized equation in (b), far fewer were able to use the complement to find the correct z-score. Others used 0.8 as the z-score. A common confusion when approaching parts (a) and (b) was whether to use a probability or a z-score. Additionally, many candidates seemed unsure of appropriate notation on this problem which would have allowed them to better demonstrate their method.

