| Date | May 2008 | Marks available | 5 | Reference code | 08M.2.sl.TZ1.8 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Copy and complete and Find | Question number | 8 | Adapted from | N/A |
Question
A box contains a large number of biscuits. The weights of biscuits are normally distributed with mean \(7{\text{ g}}\) and standard deviation \(0.5{\text{ g}}\) .
One biscuit is chosen at random from the box. Find the probability that this biscuit
(i) weighs less than \(8{\text{ g}}\) ;
(ii) weighs between \(6{\text{ g}}\) and \(8{\text{ g}}\) .
Five percent of the biscuits in the box weigh less than d grams.
(i) Copy and complete the following normal distribution diagram, to represent this information, by indicating d, and shading the appropriate region.
(ii) Find the value of d.
The weights of biscuits in another box are normally distributed with mean \(\mu \) and standard deviation \(0.5{\text{ g}}\). It is known that \(20\% \) of the biscuits in this second box weight less than \(5{\text{ g}}\).
Find the value of \(\mu \) .
Markscheme
\(X \sim {\text{N}}(7{\text{, }}{0.5^2})\)
(i) \(z = 2\) (M1)
\({\rm{P}}(X < 8) = {\rm{P}}(Z < 2) = 0.977\) A1 N2
(ii) evidence of appropriate approach (M1)
e.g. symmetry, \(z = - 2\)
\({\rm{P}}(6 < X < 8) = 0.954\) (tables 0.955) A1 N2
Note: Award M1A1(AP) if candidates refer to 2 standard deviations from the mean, leading to 0.95.
[4 marks]
(i)
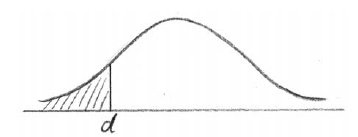 A1A1 N2
A1A1 N2
Note: Award A1 for d to the left of the mean, A1 for area to the left of d shaded.
(ii) \(z = - 1.645\) (A1)
\(\frac{{d - 7}}{{0.5}} = - 1.645\) (M1)
\(d = 6.18\) A1 N3
[5 marks]
\(Y \sim {\text{N}}(\mu {\text{, }}{0.5^2})\)
\({\rm{P}}(Y < 5) = 0.2\) (M1)
\(z = - 0.84162 \ldots \) A1
\(\frac{{5 - \mu }}{{0.5}} = - 0.8416\) (M1)
\(\mu = 5.42\) A1 N3
[4 marks]
Examiners report
Those that understood the normal distribution did well on parts (a) and (bi).
Those that understood the normal distribution did well on parts (a) and (bi). Parts (bii) and (c) proved to be a little more difficult. In particular, in part (bii) the z-score was incorrectly set equal to 0.05 and in part (c), 0.2 was used instead of the z-score. For those who had a good grasp of the concept of normal distributions the entire question was quite accessible and full marks were gained.
Those that understood the normal distribution did well on parts (a) and (bi). Parts (bii) and (c) proved to be a little more difficult. In particular, in part (bii) the z-score was incorrectly set equal to 0.05 and in part (c), 0.2 was used instead of the z-score. For those who had a good grasp of the concept of normal distributions the entire question was quite accessible and full marks were gained.

