| Date | May 2011 | Marks available | 3 | Reference code | 11M.2.sl.TZ1.4 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
A random variable X is distributed normally with a mean of 20 and variance 9.
Find \({\rm{P}}(X \le 24.5)\) .
Let \({\rm{P}}(X \le k) = 0.85\) .
(i) Represent this information on the following diagram.
(ii) Find the value of k .
Markscheme
\(\sigma = 3\) (A1)
evidence of attempt to find \({\rm{P}}(X \le 24.5)\) (M1)
e.g. \(z = 1.5\) , \(\frac{{24.5 - 20}}{3}\)
\({\rm{P}}(X \le 24.5) = 0.933\) A1 N3
[3 marks]
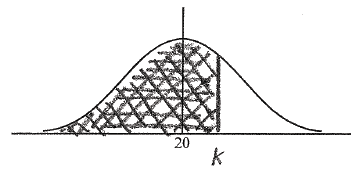 A1A1 N2
A1A1 N2
Note: Award A1 with shading that clearly extends to right of the mean, A1 for any correct label, either k, area or their value of k.
(ii) \(z = 1.03(64338)\) (A1)
attempt to set up an equation (M1)
e.g. \(\frac{{k - 20}}{3} = 1.0364\) , \(\frac{{k - 20}}{3} = 0.85\)
\(k = 23.1\) A1 N3
[5 marks]
Examiners report
This question clearly demonstrated that some centres are still not giving adequate treatment to this topic. A great many candidates neglected to find the standard deviation and used the variance throughout. More still did not leave their answers to the required accuracy. Ignoring the use of the variance, responses to part (a) demonstrated that most candidates were comfortable finding the required probability using their calculator or setting up a suitable standardized equation.
This question clearly demonstrated that some centres are still not giving adequate treatment to this topic. A great many candidates neglected to find the standard deviation and used the variance throughout. More still did not leave their answers to the required accuracy. Ignoring the use of the variance, responses to part (a) demonstrated that most candidates were comfortable finding the required probability using their calculator or setting up a suitable standardized equation. In part (b) (i), the sketch was often poorly shaded or incorrectly labelled. In (b) (ii), candidates frequently confused the z-score with the given probability of 0.85. Calculator approaches were more successful than working by hand but candidates should remember to avoid the use of calculator notation in their working, as it is not correct mathematical notation.

