| Date | November 2009 | Marks available | 2 | Reference code | 09N.1.sl.TZ0.3 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
Let X be normally distributed with mean 100 cm and standard deviation 5 cm.
On the diagram below, shade the region representing \({\rm{P}}(X > 105)\) .
Given that \({\rm{P}}(X < d) = {\rm{P}}(X > 105)\) , find the value of \(d\) .
Given that \({\rm{P}}(X > 105) = 0.16\) (correct to two significant figures), find \({\rm{P}}(d < X < 105)\) .
Markscheme
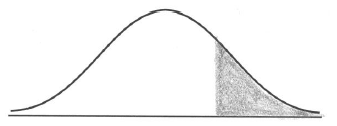 A1A1 N2
A1A1 N2
Note: Award A1 for vertical line to right of mean, A1 for shading to right of their vertical line.
evidence of recognizing symmetry (M1)
e.g. \(105\) is one standard deviation above the mean so \(d\) is one standard deviation below the mean, shading the corresponding part, \(105 - 100 = 100 - d\)
\(d = 95\) A1 N2
[2 marks]
evidence of using complement (M1)
e.g. \(1 - 0.32\) , \(1 - p\)
\({\rm{P}}(d < X < 105) = 0.68\) A1 N2
[2 marks]
Examiners report
Most candidates did very well on part (a), shading the area under the normal curve.
Not all candidates realised that the problem could be solved by only using the symmetry of the normal distribution curve and the information given. Some of them saw the need to use tables and others just left it blank.
Candidates were only moderately successful on parts (b) and (c), which required understanding of the symmetry of the curve. Many candidates resorted to formulae or tables instead of reasoning through the question.
Not all candidates realised that the problem could be solved by only using the symmetry of the normal distribution curve and the information given. Some of them saw the need to use tables and others just left it blank.
Candidates were only moderately successful on parts (b) and (c), which required understanding of the symmetry of the curve. Many candidates resorted to formulae or tables instead of reasoning through the question.

