| Date | May 2011 | Marks available | 3 | Reference code | 11M.1.sl.TZ1.10 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Write down | Question number | 10 | Adapted from | N/A |
Question
The velocity v ms−1 of a particle at time t seconds, is given by \(v = 2t + \cos 2t\) , for \(0 \le t \le 2\) .
Write down the velocity of the particle when \(t = 0\) .
When \(t = k\) , the acceleration is zero.
(i) Show that \(k = \frac{\pi }{4}\) .
(ii) Find the exact velocity when \(t = \frac{\pi }{4}\) .
When \(t < \frac{\pi }{4}\) , \(\frac{{{\rm{d}}v}}{{{\rm{d}}t}} > 0\) and when \(t > \frac{\pi }{4}\) , \(\frac{{{\rm{d}}v}}{{{\rm{d}}t}} > 0\) .
Sketch a graph of v against t .
Let d be the distance travelled by the particle for \(0 \le t \le 1\) .
(i) Write down an expression for d .
(ii) Represent d on your sketch.
Markscheme
\(v = 1\) A1 N1
[1 mark]
(i) \(\frac{{\rm{d}}}{{{\rm{d}}t}}(2t) = 2\) A1
\(\frac{{\rm{d}}}{{{\rm{d}}t}}(\cos 2t) = - 2\sin 2t\) A1A1
Note: Award A1 for coefficient 2 and A1 for \( - \sin 2t\) .
evidence of considering acceleration = 0 (M1)
e.g. \(\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = 0\) , \(2 - 2\sin 2t = 0\)
correct manipulation A1
e.g. \(\sin 2k = 1\) , \(\sin 2t = 1\)
\(2k = \frac{\pi }{2}\) (accept \(2t = \frac{\pi }{2}\) ) A1
\(k = \frac{\pi }{4}\) AG N0
(ii) attempt to substitute \(t = \frac{\pi }{4}\) into v (M1)
e.g. \(2\left( {\frac{\pi }{4}} \right) + \cos \left( {\frac{{2\pi }}{4}} \right)\)
\(v = \frac{\pi }{2}\) A1 N2
[8 marks]
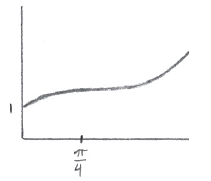 A1A1A2 N4
A1A1A2 N4
Notes: Award A1 for y-intercept at \((0{\text{, }}1)\) , A1 for curve having zero gradient at \(t = \frac{\pi }{4}\) , A2 for shape that is concave down to the left of \(\frac{\pi }{4}\) and concave up to the right of \(\frac{\pi }{4}\) . If a correct curve is drawn without indicating \(t = \frac{\pi }{4}\) , do not award the second A1 for the zero gradient, but award the final A2 if appropriate. Sketch need not be drawn to scale. Only essential features need to be clear.
[4 marks]
(i) correct expression A2
e.g. \(\int_0^1 {(2t + \cos 2t){\rm{d}}t} \) , \(\left[ {{t^2} + \frac{{\sin 2t}}{2}} \right]_0^1\) , \(1 + \frac{{\sin 2}}{2}\) , \(\int_0^1 {v{\rm{d}}t} \)
(ii)
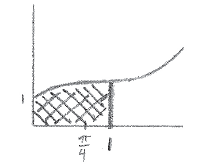 A1
A1
Note: The line at \(t = 1\) needs to be clearly after \(t = \frac{\pi }{4}\) .
[3 marks]
Examiners report
Many candidates gave a correct initial velocity, although a substantial number of candidates answered that \(0 + \cos 0 = 0\) .
For (b), students commonly applied the chain rule correctly to achieve the derivative, and many recognized that the acceleration must be zero. Occasionally a student would use a double-angle identity on the velocity function before differentiating. This is not incorrect, but it usually caused problems when trying to show \(k = \frac{\pi }{4}\) . At times students would reach the equation \(\sin 2k = 1\) and then substitute the \(\frac{\pi }{4}\) , which does not satisfy the “show that” instruction.
The challenge in this question is sketching the graph using the information achieved and provided. This requires students to make graphical interpretations, and as typical in section B, to link the early parts of the question with later parts. Part (a) provides the y-intercept, and part (b) gives a point with a horizontal tangent. Plotting these points first was a helpful strategy. Few understood either the notation or the concept that the function had to be increasing on either side of the \(\frac{\pi }{4}\) , with most thinking that the point was either a max or min. It was the astute student who recognized that the derivatives being positive on either side of \(\frac{\pi }{4}\) creates a point of inflexion.
Additionally, important points should be labelled in a sketch. Indicating the \(\frac{\pi }{4}\) on the x-axis is a requirement of a clear graph. Although students were not penalized for not labelling the \(\frac{\pi }{2}\) on the y-axis, there should be a recognition that the point is higher than the y-intercept.
While some candidates recognized that the distance is the area under the velocity graph, surprisingly few included neither the limits of integration in their expression, nor the “dt”. Most unnecessarily attempted to integrate the function, often giving an answer with “+C”, and only earned marks if the limits were included with their result. Few recognized that a shaded area is an adequate representation of distance on the sketch, with most fruitlessly attempting to graph a new curve.

