IB Questionbank

User interface language: English | Español

Date	November 2015	Marks available	3	Reference code	15N.2.sl.TZ0.6
Level	SL only	Paper	2	Time zone	TZ0
Command term	Find	Question number	6	Adapted from	N/A

Question

The velocity $v{\text{ m}}{{\text{s}}^{ - 1}}$ of a particle after $t$ seconds is given by

$v(t) = {(0.3t + 0.1)^t} - 4$ , for $0 \le t \le 5$

The following diagram shows the graph of $v$ .

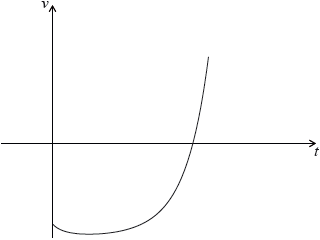
Find the value of $t$ when the particle is at rest.

[3]

Find the value of $t$ when the acceleration of the particle is $0$ .

[3]

Markscheme

recognizing particle at rest when $v = 0$ (M1)

eg $\;\;\;{(0.3t + 0.1)^t} - 4 = 0$ , $x$ -intercept on graph of $v$

$t = 4.27631$

$t = 4.28{\text{ }} {\text{ (seconds)}}$ A2 N3

[3 marks]

valid approach to find $t$ when $a$ is $0$ (M1)

eg $\;\;\;v'(t) = 0$ , $v$ minimum

$t = 1.19236$

$t = 1.19{\text{ }}{\text{ (seconds)}}$ A2 N3

[3 marks]

Total [6 marks]

Examiners report

[N/A]

Syllabus sections

Topic 6 - Calculus » 6.6 » Kinematic problems involving displacement

$s$ , velocity

$v$ and acceleration

$a$ .

Show 53 related questions

17N.2.sl.TZ0.9d: Find the total distance travelled by P when its velocity is increasing.
17N.2.sl.TZ0.9c: Find an expression for the velocity of P at time $t$ .
17N.2.sl.TZ0.9b: Hence or otherwise, find all possible values of $t$ for which the velocity of P is decreasing.
17N.2.sl.TZ0.9a: Write down the values of $t$ when $a = 0$ .
16M.2.sl.TZ2.7: A particle moves in a straight line. Its velocity $v{\text{ m}}\,{{\text{s}}^{ - 1}}$ after...
16M.2.sl.TZ1.9e: Find the maximum speed of P.
16M.2.sl.TZ1.9d: Find the acceleration of P after 3 seconds.
16M.2.sl.TZ1.9c: Write down the number of times P changes direction.
16M.2.sl.TZ1.9b: Find when P is first at rest.
16M.2.sl.TZ1.9a: Find the displacement of P from O after 5 seconds.
16N.2.sl.TZ0.9d: (i) Find the total distance travelled by P between $t = 1$ and $t = p$ . (ii) ...
16N.2.sl.TZ0.9c: (i) Find the value of $q$ . (ii) Hence, find the speed of P when $t = q$ .
16N.2.sl.TZ0.9b: Find the value of $p$ .
16N.2.sl.TZ0.9a: Find the initial velocity of $P$ .
12N.2.sl.TZ0.7a: On the grid below, sketch the graph of $s$ .
12N.2.sl.TZ0.7b: Find the maximum velocity of the particle.
12M.2.sl.TZ2.5a: Find the acceleration of the particle after 2.7 seconds.
12M.2.sl.TZ2.5b: Find the displacement of the particle after 1.3 seconds.
08N.1.sl.TZ0.9a: Find the acceleration of the particle at $t = 0$ .
08N.1.sl.TZ0.9b: Find the velocity, v, at time t, given that the initial velocity of the particle is...
08N.1.sl.TZ0.9c: Find $\int_0^3 {v{\rm{d}}t}$ , giving your answer in the form $p - q\cos 3$ .
08N.1.sl.TZ0.9d: What information does the answer to part (c) give about the motion of the particle?
08M.1.sl.TZ1.6: A particle moves along a straight line so that its velocity,...
12M.1.sl.TZ1.10a: Find $s'(t)$ .
12M.1.sl.TZ1.10b: In this interval, there are only two values of t for which the object is not moving. One...
12M.1.sl.TZ1.10c: Show that $s'(t) > 0$ between these two values of t .
12M.1.sl.TZ1.10d: Find the distance travelled between these two values of t .
09M.1.sl.TZ1.4b: Write down the value of t when the velocity is greatest.
09M.1.sl.TZ1.4a: Complete the following table by noting which graph A, B or C corresponds to each function.
09M.1.sl.TZ2.11a: (i) If $s = 100$ when $t = 0$ , find an expression for s in terms of a and...
09M.1.sl.TZ2.11b: A train M slows down so that it comes to a stop at the station. (i) Find the time it...
09M.1.sl.TZ2.11c: For a different train N, the value of a is 4. Show that this train will stop before it...
10M.2.sl.TZ1.6: The acceleration, $a{\text{ m}}{{\text{s}}^{ - 2}}$ , of a particle at time t seconds is...
SPNone.1.sl.TZ0.3a: Write down the car’s velocity at $t = 3$ .
SPNone.1.sl.TZ0.3b: Find the car’s acceleration at $t = 1.5$ .
11M.1.sl.TZ1.10b(i) and (ii): When $t = k$ , the acceleration is zero. (i) Show that $k = \frac{\pi }{4}$ . (ii)...
11M.1.sl.TZ1.10c: When $t < \frac{\pi }{4}$ , $\frac{{{\rm{d}}v}}{{{\rm{d}}t}} > 0$ and when...
11M.1.sl.TZ1.10d(i) and (ii): Let d be the distance travelled by the particle for $0 \le t \le 1$ . (i) Write down...
11M.1.sl.TZ1.10a: Write down the velocity of the particle when $t = 0$ .
11M.1.sl.TZ2.9a: Write down $f(x)$ in the form $f(x) = - 10(x - p)(x - q)$ .
11M.1.sl.TZ2.9b: Find another expression for $f(x)$ in the form $f(x) = - 10{(x - h)^2} + k$ .
11M.1.sl.TZ2.9c: Show that $f(x)$ can also be written in the form $f(x) = 240 + 20x - 10{x^2}$ .
11M.1.sl.TZ2.9d(i) and (ii): A particle moves along a straight line so that its velocity,...
13M.1.sl.TZ2.6: A rocket moving in a straight line has velocity $v$ km s–1 and displacement $s$ km at...
14M.2.sl.TZ1.6: Ramiro and Lautaro are travelling from Buenos Aires to El Moro. Ramiro travels in a vehicle...
14M.2.sl.TZ2.9a: Find the velocity of the particle when $t = 1$ .
14M.2.sl.TZ2.9b: Find the value of $t$ for which the particle is at rest.
14M.2.sl.TZ2.9c: Find the total distance the particle travels during the first three seconds.
14M.2.sl.TZ2.9d: Show that the acceleration of the particle is given by $a = 6t{({t^2} - 4)^2}$ .
14M.2.sl.TZ2.9e: Find all possible values of $t$ for which the velocity and acceleration are both positive...
13N.2.sl.TZ0.5c: Find the velocity of the particle when its acceleration is zero.
14N.2.sl.TZ0.7a: Find the distance travelled by the particle for $0 \le t \le\ \frac{\pi }{2}$ .
15N.2.sl.TZ0.6b: Find the value of $t$ when the acceleration of the particle is $0$ .

Hide related questions

Question

Markscheme

Examiners report

Syllabus sections

View options