| Date | November 2014 | Marks available | 2 | Reference code | 14N.2.sl.TZ0.7 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
A particle starts from point \(A\) and moves along a straight line. Its velocity, \(v\;{\text{m}}{{\text{s}}^{ - 1}}\), after \(t\) seconds is given by \(v(t) = {{\text{e}}^{\frac{1}{2}\cos t}} - 1\), for \(0 \le t \le 4\). The particle is at rest when \(t = \frac{\pi }{2}\).
The following diagram shows the graph of \(v\).
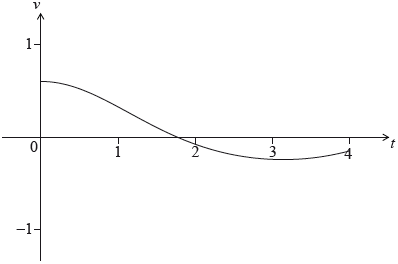
Find the distance travelled by the particle for \(0 \le t \le\ \frac{\pi }{2}\).
Explain why the particle passes through \(A\) again.
Markscheme
correct substitution of function and/or limits into formula (A1)
(accept absence of d\(t\), but do not accept any errors)
eg\(\;\;\;\)\(\int_0^{\frac{\pi }{2}} {v,{\text{ }}\int {\left| {{{\text{e}}^{\frac{1}{2}\cos t}} - 1} \right|{\text{d}}t,{\text{ }}\int {\left( {{{\text{e}}^{\frac{1}{2}\cos t}} - 1} \right)} } } \)
\(0.613747\)
distance is \(0.614{\text{ }}[0.613,{\text{ }}0.614]{\text{ (m)}}\) A1 N2
[2 marks]
METHOD 1
valid attempt to find the distance travelled between \(t = \frac{\pi }{2}\) and \(t = 4\) (M1)
eg\(\;\;\;\)\(\int_{\frac{\pi }{2}}^4 {\left( {{{\text{e}}^{\frac{1}{2}\cos t}} - 1} \right),{\text{ }}\int_0^4 {\left| {{{\text{e}}^{\frac{1}{2}\cos t}} - 1} \right|{\text{d}}t - 0.614} } \)
distance is \(0.719565\) A1
valid reason, referring to change of direction (may be seen in explanation) R1
valid explanation comparing their distances R1
eg\(\;\;\;\)\(0.719565 > 0.614\), distance moving back is more than distance moving forward
Note: Do not award the final R1 unless the A1 is awarded.
particle passes through \(A\) again AG N0
METHOD 2
valid attempt to find displacement (M1)
eg\(\;\;\;\)\(\int_{\frac{\pi }{2}}^4 {\left( {{{\text{e}}^{\frac{1}{2}\cos t}} - 1} \right),{\text{ }}\int_0^4 {\left( {{{\text{e}}^{\frac{1}{2}\cos t}} - 1} \right)} } \)
correct displacement A1
eg\(\;\;\;\)\(-0.719565,{\text{ }}-0.105817\)
recognizing that displacement from \(0\) to \(\frac{\pi }{2}\) is positive R1
eg\(\;\;\;\)displacement = distance from \(0\) to \(\frac{\pi }{2}\)
valid explanation referring to positive and negative displacement R1
eg\(\;\;\;\)\(0.719565 > 0.614\), overall displacement is negative, since displacement after \(\frac{\pi }{2}\) is negative, then particle gone backwards more than forwards
Note: Do not award the final R1 unless the A1 and the first R1 are awarded.
particle passes through A\(A\) again AG N0
[4 marks]
Note: Special Case.
If all working shown, and candidates seem to have misread the question, using [equation], award marks as follows:
(a) correct substitution of function and/or limits into formula (accept absence of dt, but do not accept any errors) A0MR
eg [equation]
\(2.184544\)
distance is \(2.18\) [\(2.18\), \(2.19\)] (m) A1 N0
(b) METHOD 1
valid attempt to find the distance travelled between [equation] M1
eg [equation]
distance is \(1.709638\) A1
reference to change of direction (may be seen in explanation) R1
reasoning/stating particle passes/does not pass through \(A\) again R0
METHOD 2
valid attempt to find displacement M1
eg [equation]
correct displacement A1
eg \(1.709638,{\rm{ }}3.894182\)
recognising that displacement from [ \(0\) to (pi/2] is positive R0
reasoning/stating particle passes/does not pass through \(A\) again R0
With method 2, there is no valid reasoning about whether the particle passes through \(A\) again or not, so they cannot gain the R marks.
Total [6 marks]
Examiners report
For part (a), a large number of candidates chose the correct formula to find the distance but many got an incorrect value. A considerable number of candidates misread the function as \(v(t) = {{\text{e}}^{\frac{1}{2}\cos t}}\), losing a mark for this part.
Only a few candidates gained full marks in part (b). Although many mentioned the change of direction, very few supported their answer with a calculation of the distance travelled back or the displacement, thus showing poor understanding of the command term “explain”.
The periodic nature of the function confused many candidates, who used this fact to assure that the particle would pass through A again.

