| Date | November 2015 | Marks available | 5 | Reference code | 15N.1.sl.TZ0.8 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
The following diagram shows part of the graph of a quadratic function \(f\).
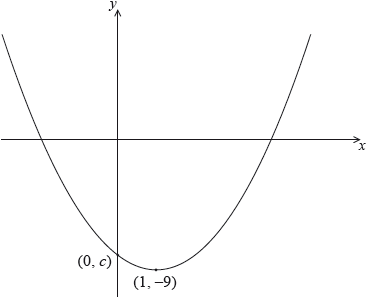
The vertex is at \((1,{\text{ }} - 9)\), and the graph crosses the y-axis at the point \((0,{\text{ }}c)\).
The function can be written in the form \(f(x) = {(x - h)^2} + k\).
Write down the value of \(h\) and of \(k\).
Find the value of \(c\).
Let \(g(x) = - {(x - 3)^2} + 1\). The graph of \(g\) is obtained by a reflection of the graph of \(f\) in the \(x\)-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}} p \\ q \end{array}} \right)\).
Find the value of \(p\) and of \(q\).
Find the x-coordinates of the points of intersection of the graphs of \(f\) and \(g\).
Markscheme
\(h = 1,{\text{ }}k = - 9\;\;\;\left( {{\text{accept }}{{(x - 1)}^2} - 9} \right)\) A1A1 N2
[2 marks]
METHOD 1
attempt to substitute \(x = 0\) into their quadratic function (M1)
eg\(\;\;\;f(0),{\text{ }}{(0 - 1)^2} - 9\)
\(c = - 8\) A1 N2
METHOD 2
attempt to expand their quadratic function (M1)
eg\(\;\;\;{x^2} - 2x + 1 - 9,{\text{ }}{x^2} - 2x - 8\)
\(c = - 8\) A1 N2
[2 marks]
evidence of correct reflection A1
eg\(\;\;\; - \left( {{{(x - 1)}^2} - 9} \right)\), vertex at \((1,{\text{ }}9)\), y-intercept at \((0,{\text{ }}8)\)
valid attempt to find horizontal shift (M1)
eg\(\;\;\;1 + p = 3,{\text{ }}1 \to 3\)
\(p = 2\) A1 N2
valid attempt to find vertical shift (M1)
eg\(\;\;\;9 + q = 1,{\text{ }}9 \to 1,{\text{ }} - 9 + q = 1\)
\(q = - 8\) A1 N2
Notes: An error in finding the reflection may still allow the correct values of \(p\) and \(q\) to be found, as the error may not affect subsequent working. In this case, award A0 for the reflection, M1A1 for \(p = 2\), and M1A1 for \(q = - 8\).
If no working shown, award N0 for \(q = 10\).
[5 marks]
valid approach (check FT from (a)) M1
eg\(\;\;\;f(x) = g(x),{\text{ }}{(x - 1)^2} - 9 = - {(x - 3)^2} + 1\)
correct expansion of both binomials (A1)
eg\(\;\;\;{x^2} - 2x + 1,{\text{ }}{x^2} - 6x + 9\)
correct working (A1)
eg\(\;\;\;{x^2} - 2x - 8 = - {x^2} + 6x - 8\)
correct equation (A1)
eg\(\;\;\;2{x^2} - 8x = 0,{\text{ }}2{x^2} = 8x\)
correct working (A1)
eg\(\;\;\;2x(x - 4) = 0\)
\(x = 0,{\text{ }}x = 4\) A1A1 N3
[7 marks]
Total [16 marks]

