| Date | May 2012 | Marks available | 2 | Reference code | 12M.1.sl.TZ2.5 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Sketch | Question number | 5 | Adapted from | N/A |
Question
The diagram below shows the graph of a function \(f(x)\) , for \( - 2 \le x \le 3\) .
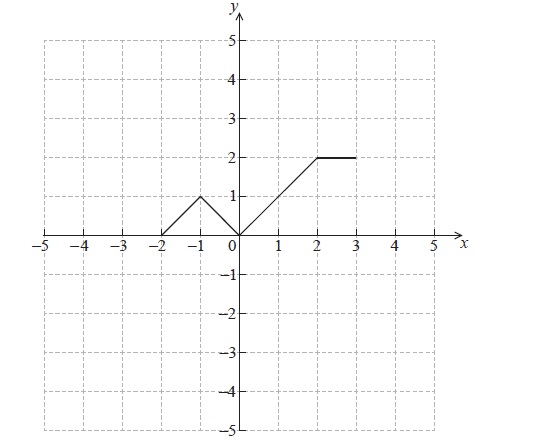
Sketch the graph of \(f( - x)\) on the grid below.
The graph of f is transformed to obtain the graph of g . The graph of g is shown below.
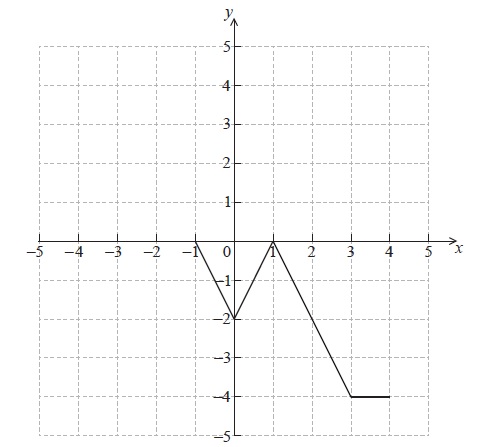
The function g can be written in the form \(g(x) = af(x + b)\) . Write down the value of a and of b .
Markscheme
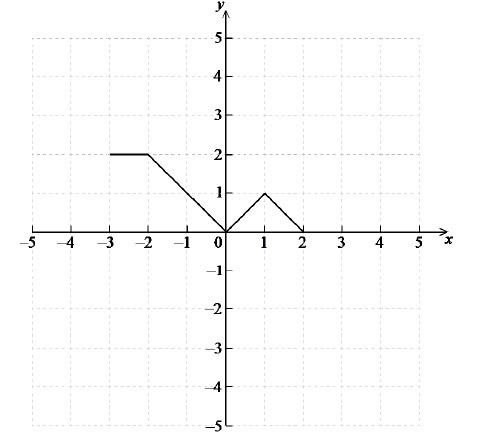 A2 N2
A2 N2
[2 marks]
\(a = - 2,b = - 1\) A2A2 N4
Note: Award A1 for \(a = 2\) , A1 for \(b = 1\) .
[4 marks]
Examiners report
In part (a) of this question, a large number of candidates correctly sketched the graph of \(f( - x)\) , as asked. A fairly common error, however, was to graph \( - f(x)\) .
In part (b), many candidates seemed to recognize that the value of a was related to a vertical stretch, though some omitted the negative required for the vertical reflection. Similarly, some candidates gave a positive value for b.

