| Date | May 2008 | Marks available | 2 | Reference code | 08M.1.sl.TZ2.5 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Sketch | Question number | 5 | Adapted from | N/A |
Question
Part of the graph of a function f is shown in the diagram below.
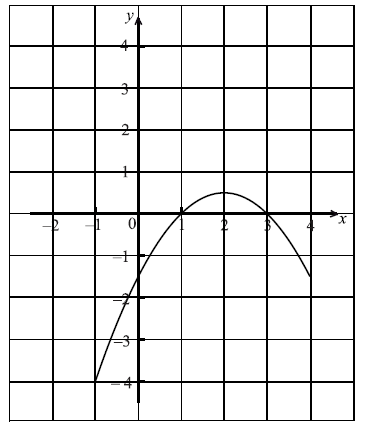
On the same diagram sketch the graph of \(y = - f(x)\) .
Let \(g(x) = f(x + 3)\) .
(i) Find \(g( - 3)\) .
(ii) Describe fully the transformation that maps the graph of f to the graph of g.
Markscheme
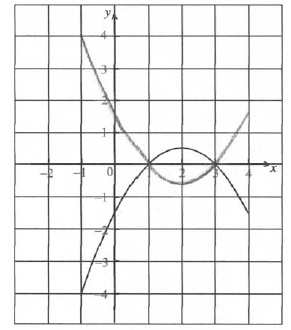 M1A1 N2
M1A1 N2
Note: Award M1 for evidence of reflection in x-axis, A1 for correct vertex and all intercepts approximately correct.
(i) \(g( - 3) = f(0)\) (A1)
\(f(0) = - 1.5\) A1 N2
(ii) translation (accept shift, slide, etc.) of \(\left( {\begin{array}{*{20}{c}}
{ - 3}\\
0
\end{array}} \right)\) A1A1 N2
[4 marks]
Examiners report
This question was reasonably well done. Many recognized the graph of \( - f(x)\) as a reflection in a horizontal line, but fewer recognized the x-axis as the mirror line.
A fair number gave \(g( - 3) = f(0)\) , but did not carry through to \(f(0) = - 1.5\) . The majority of candidates recognized that moving the graph of \(f(x)\) by 3 units to the left results in the graph of \(g(x)\) , but the language used to describe the transformation was often far from precise mathematically.

