| Date | November 2009 | Marks available | 3 | Reference code | 09N.1.sl.TZ0.4 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The diagram below shows the graph of a function \(f(x)\) , for \( - 2 \le x \le 4\) .
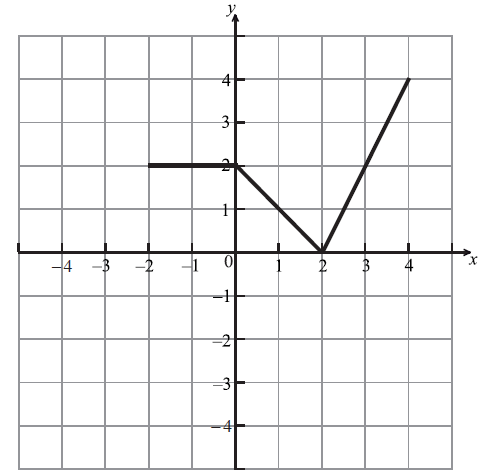
Let \(h(x) = f( - x)\) . Sketch the graph of \(h\) on the grid below.
Let \(g(x) = \frac{1}{2}f(x - 1)\) . The point \({\text{A}}(3{\text{, }}2)\) on the graph of \(f\) is transformed to the point P on the graph of \(g\) . Find the coordinates of P.
Markscheme
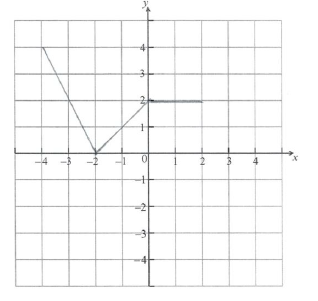 A2 N2
A2 N2
[2 marks]
evidence of appropriate approach (M1)
e.g. reference to any horizontal shift and/or stretch factor, \(x = 3 + 1\) , \(y = \frac{1}{2} \times 2\)
P is \((4{\text{, }}1)\) (accept \(x = 4\) , \(y = 1\)) A1A1 N3
[3 marks]
Examiners report
Part (a) was generally solved correctly. Students had no trouble in deciding what transformation had to be done to the graph, although some confused \(f( - x)\) with \( - f(x)\) .
Part (b) was generally poorly done. They could not "read" that the transformation shifted the curve 1 unit to the right and stretched it in the \(y\)-direction with a scale factor of \(\frac{1}{2}\) . It was often seen that the shift was interpreted, but in the opposite direction. Also, the stretch was applied to both coordinates of the point. Those candidates who answered part (a) incorrectly often had trouble on (b) as well, indicating a difficulty with transformations in general. However, there were also candidates who solved part (a) correctly but could not interpret part (b). This would indicate that it is simpler for them to plot the transformation of an entire function than to find how a particular point is transformed.

