| Date | November 2009 | Marks available | 3 | Reference code | 09N.2.sl.TZ0.9 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Sketch | Question number | 9 | Adapted from | N/A |
Question
Let \(f(x) = 5\cos \frac{\pi }{4}x\) and \(g(x) = - 0.5{x^2} + 5x - 8\) for \(0 \le x \le 9\) .
On the same diagram, sketch the graphs of f and g .
Consider the graph of \(f\) . Write down
(i) the x-intercept that lies between \(x = 0\) and \(x = 3\) ;
(ii) the period;
(iii) the amplitude.
Consider the graph of g . Write down
(i) the two x-intercepts;
(ii) the equation of the axis of symmetry.
Let R be the region enclosed by the graphs of f and g . Find the area of R.
Markscheme
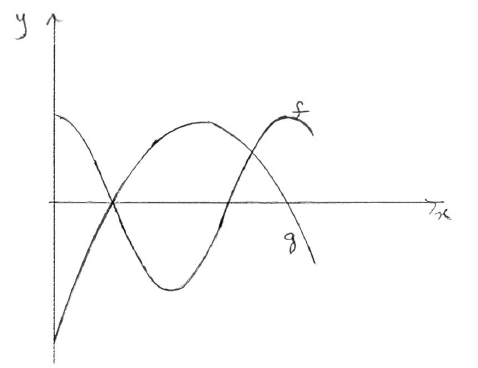 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for f being of sinusoidal shape, with 2 maxima and one minimum, A1 for g being a parabola opening down, A1 for two intersection points in approximately correct position.
[3 marks]
(i) \((2{\text{, }}0)\) (accept \(x = 2\) ) A1 N1
(ii) \({\text{period}} = 8\) A2 N2
(iii) \({\text{amplitude}} = 5\) A1 N1
[4 marks]
(i) \((2{\text{, }}0)\) , \((8{\text{, }}0)\) (accept \(x = 2\) , \(x = 8\) ) A1A1 N1N1
(ii) \(x = 5\) (must be an equation) A1 N1
[3 marks]
METHOD 1
intersect when \(x = 2\) and \(x = 6.79\) (may be seen as limits of integration) A1A1
evidence of approach (M1)
e.g. \(\int {g - f} \) , \(\int {f(x){\rm{d}}x - \int {g(x){\rm{d}}x}}\) , \(\int_2^{6.79} {\left( {( - 0.5{x^2} + 5x - 8) - \left( {5\cos \frac{\pi }{4}x} \right)} \right)}\)
\({\text{area}} = 27.6\) A2 N3
METHOD 2
intersect when \(x = 2\) and \(x = 6.79\) (seen anywhere) A1A1
evidence of approach using a sketch of g and f , or \(g - f\) . (M1)
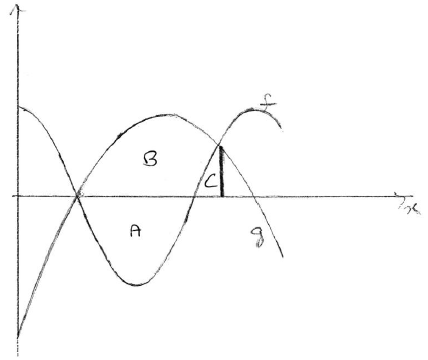
e.g. area = \(A + B - C\) , \(12.7324 + 16.0938 - 1.18129 \ldots \)
\({\text{area}} = 27.6\) A2 N3
[5 marks]
Examiners report
Graph sketches were much improved over previous sessions. Most candidates graphed the two functions correctly, but many ignored the domain restrictions.
Many candidates found parts (b) and (c) accessible, although quite a few did not know how to find the period of the cosine function.
Many candidates found parts (b) and (c) accessible, although quite a few did not know how to find the period of the cosine function.
Part (d) proved elusive to many candidates. Some used creative approaches that split the area into parts above and below the x-axis; while this leads to a correct result, few were able to achieve it. Many candidates were unable to use their GDCs effectively to find points of intersection and the subsequent area.

