| Date | May 2015 | Marks available | 3 | Reference code | 15M.2.sl.TZ1.5 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Sketch | Question number | 5 | Adapted from | N/A |
Question
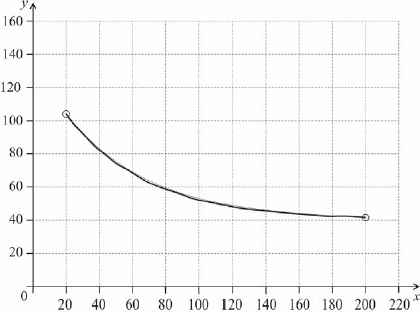
Let \(G(x) = 95{{\text{e}}^{( - 0.02x)}} + 40\), for \(20 \le x \le 200\).
On the following grid, sketch the graph of \(G\).
Robin and Pat are planning a wedding banquet. The cost per guest, \(G\) dollars, is modelled by the function \(G(n) = 95{{\text{e}}^{( - 0.02n)}} + 40\), for \(20 \le n \le 200\), where \(n\) is the number of guests.
Calculate the total cost for \(45\) guests.
Markscheme
 A1A1A1 N3
A1A1A1 N3
Note: Curve must be approximately correct exponential shape (concave up and decreasing). Only if the shape is approximately correct, award the following:
A1 for left endpoint in circle,
A1 for right endpoint in circle,
A1 for asymptotic to \(y = 40\) (must not go below \(y = 40\)).
[3 marks]
attempt to find \(G(45)\) (M1)
eg\(\;\;\;78.6241\), value read from their graph
multiplying cost times number of people (M1)
eg\(\;\;\;45 \times 78.6241,{\text{ }}G(45) \times 45\)
\(3538.08\)
\(3540\) (dollars) A1 N2
[3 marks]
Total [6 marks]
Examiners report
The majority of candidates were able to sketch the shape of the graph accurately, but graph sketching is an area of the syllabus in which candidates continue to lose marks. In this particular question, candidates often did not consider the given domain or failed to accurately show the behaviour of the graph close to the horizontal asymptote as \(x \to \infty \).
In (b), most candidates were able to identify the initial approach by finding \(G(45)\), but missed the fact that function defined the cost per guest and not the total cost.

