| Date | May 2014 | Marks available | 3 | Reference code | 14M.2.sl.TZ1.9 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Sketch | Question number | 9 | Adapted from | N/A |
Question
Let \(f(x) = \cos \left( {\frac{\pi }{4}x} \right) + \sin \left( {\frac{\pi }{4}x} \right),{\text{ for }} - 4 \leqslant x \leqslant 4.\)
Sketch the graph of \(f\).
Find the values of \(x\) where the function is decreasing.
The function \(f\) can also be written in the form \(f(x) = a\sin \left( {\frac{\pi }{4}(x + c)} \right)\), where \(a \in \mathbb{R}\), and \(0 \leqslant c \leqslant 2\). Find the value of \(a\);
The function \(f\) can also be written in the form \(f(x) = a\sin \left( {\frac{\pi }{4}(x + c)} \right)\), where \(a \in \mathbb{R}\), and \(0 \leqslant c \leqslant 2\). Find the value of \(c\).
Markscheme
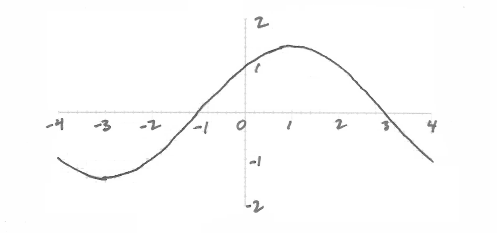 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for approximately correct sinusoidal shape.
Only if this A1 is awarded, award the following:
A1 for correct domain,
A1 for approximately correct range.
[3 marks]
recognizes decreasing to the left of minimum or right of maximum,
eg \(f'(x) < 0\) (R1)
x-values of minimum and maximum (may be seen on sketch in part (a)) (A1)(A1)
eg \(x = - 3,{\text{ (1, 1.4)}}\)
two correct intervals A1A1 N5
eg \( - 4 < x < - 3,{\text{ }}1 \leqslant x \leqslant 4;{\text{ }}x < - 3,{\text{ }}x \geqslant 1\)
[5 marks]
recognizes that \(a\) is found from amplitude of wave (R1)
y-value of minimum or maximum (A1)
eg (−3, −1.41) , (1, 1.41)
\(a = 1.41421\)
\(a = \sqrt 2 {\text{, (exact), 1.41,}}\) A1 N3
[3 marks]
METHOD 1
recognize that shift for sine is found at x-intercept (R1)
attempt to find x-intercept (M1)
eg \(\cos \left( {\frac{\pi }{4}x} \right) + \sin \left( {\frac{\pi }{4}x} \right) = 0,{\text{ }}x = 3 + 4k,{\text{ }}k \in \mathbb{Z}\)
\(x = - 1\) (A1)
\(c = 1\) A1 N4
METHOD 2
attempt to use a coordinate to make an equation (R1)
eg \(\sqrt 2 \sin \left( {\frac{\pi }{4}c} \right) = 1,{\text{ }}\sqrt 2 \sin \left( {\frac{\pi }{4}(3 - c)} \right) = 0\)
attempt to solve resulting equation (M1)
eg sketch, \(x = 3 + 4k,{\text{ }}k \in \mathbb{Z}\)
\(x = - 1\) (A1)
\(c = 1\) A1 N4
[4 marks]

