| Date | November 2011 | Marks available | 3 | Reference code | 11N.1.sl.TZ0.6 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
Let \(\sin \theta = \frac{2}{{\sqrt {13} }}\) , where \(\frac{\pi }{2} < \theta < \pi \) .
Find \(\cos \theta \) .
Find \(\tan 2\theta \) .
Markscheme
METHOD 1
evidence of choosing \({\sin ^2}\theta + {\cos ^2}\theta = 1\) (M1)
correct working (A1)
e.g. \({\cos ^2}\theta = \frac{9}{{13}}\) , \(\cos \theta = \pm \frac{3}{{\sqrt {13} }}\) , \(\cos \theta = \sqrt {\frac{9}{{13}}} \)
\(\cos \theta = - \frac{3}{{\sqrt {13} }}\) A1 N2
Note: If no working shown, award N1 for \(\frac{3}{{\sqrt {13} }}\) .
METHOD 2
approach involving Pythagoras’ theorem (M1)
e.g. \({2^2} + {x^2} = 13\) ,
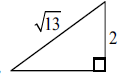
finding third side equals 3 (A1)
\(\cos \theta = - \frac{3}{{\sqrt {13} }}\) A1 N2
Note: If no working shown, award N1 for \(\frac{3}{{\sqrt {13} }}\) .
[3 marks]
correct substitution into \(\sin 2\theta \) (seen anywhere) (A1)
e.g. \(2\left( {\frac{2}{{\sqrt {13} }}} \right)\left( { - \frac{3}{{\sqrt {13} }}} \right)\)
correct substitution into \(\cos 2\theta \) (seen anywhere) (A1)
e.g. \({\left( { - \frac{3}{{\sqrt {13} }}} \right)^2} - {\left( {\frac{2}{{\sqrt {13} }}} \right)^2}\) , \(2{\left( { - \frac{3}{{\sqrt {13} }}} \right)^2} - 1\) , \(1 - 2{\left( {\frac{2}{{\sqrt {13} }}} \right)^2}\)
valid attempt to find \(\tan 2\theta \) (M1)
e.g. \(\frac{{2\left( {\frac{2}{{\sqrt {13} }}} \right)\left( { - \frac{3}{{\sqrt {13} }}} \right)}}{{{{\left( { - \frac{3}{{\sqrt {13} }}} \right)}^2} - {{\left( {\frac{2}{{\sqrt {13} }}} \right)}^2}}}\) , \(\frac{{2\left( { - \frac{2}{3}} \right)}}{{1 - {{\left( { - \frac{2}{3}} \right)}^2}}}\)
correct working A1
e.g. \(\frac{{\frac{{(2)(2)( - 3)}}{{13}}}}{{\frac{9}{{13}} - \frac{4}{{13}}}}\) , \(\frac{{ - \frac{{12}}{{{{\left( {\sqrt {13} } \right)}^2}}}}}{{\frac{{18}}{{13}} - 1}}\) , \(\frac{{ - \frac{{12}}{{13}}}}{{\frac{5}{{13}}}}\)
\(\tan 2\theta = - \frac{{12}}{5}\) A1 N4
Note: If students find answers for \(\cos \theta \) which are not in the range \([ - 1{\text{, }}1]\), award full FT in (b) for correct FT working shown.
[5 marks]
Examiners report
While the majority of candidates knew to use the Pythagorean identity in part (a), very few remembered that the cosine of an angle in the second quadrant will have a negative value.
In part (b), many candidates incorrectly tried to calculate \(\tan 2\theta \) as \(2 \times \tan \theta \) , rather than using the double-angle identities.

