| Date | May 2008 | Marks available | 3 | Reference code | 08M.1.sl.TZ2.4 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
Given that \(\cos A = \frac{1}{3}\) and \(0 \le A \le \frac{\pi }{2}\) , find \(\cos 2A\) .
Given that \(\sin B = \frac{2}{3}\) and \(\frac{\pi }{2} \le B \le \pi \) , find \(\cos B\) .
Markscheme
evidence of choosing the formula \(\cos 2A = 2{\cos ^2}A - 1\) (M1)
Note: If they choose another correct formula, do not award the M1 unless there is evidence of finding \({\sin ^2}A = 1 - \frac{1}{9}\)
correct substitution A1
e.g.\(\cos 2A = {\left( {\frac{1}{3}} \right)^2} - \frac{8}{9}\) , \(\cos 2A = 2 \times {\left( {\frac{1}{3}} \right)^2} - 1\)
\(\cos 2A = - \frac{7}{9}\) A1 N2
[3 marks]
METHOD 1
evidence of using \({\sin ^2}B + {\cos ^2}B = 1\) (M1)
e.g. \({\left( {\frac{2}{3}} \right)^2} + {\cos ^2}B = 1\) , \(\sqrt {\frac{5}{9}} \) (seen anywhere),
\(\cos B = \pm \sqrt {\frac{5}{9}} \) \(\left( { = \pm \frac{{\sqrt 5 }}{3}} \right)\) (A1)
\(\cos B = - \sqrt {\frac{5}{9}} \) \(\left( { = - \frac{{\sqrt 5 }}{3}} \right)\) A1 N2
METHOD 2
diagram M1
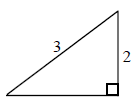
for finding third side equals \(\sqrt 5 \) (A1)
\(\cos B = - \frac{{\sqrt 5 }}{3}\) A1 N2
[3 marks]
Examiners report
This question was very poorly done, and knowledge of basic trigonometric identities and values of trigonometric functions of obtuse angles seemed distinctly lacking. Candidates who recognized the need of an identity for finding \(\cos 2A\) given \(\cos A\) seldom chose the most appropriate of the three and even when they did often used it incorrectly with expressions such as \(2{\cos ^2}\frac{1}{9} - 1\) .
This question was very poorly done, and knowledge of basic trigonometric identities and values of trigonometric functions of obtuse angles seemed distinctly lacking. Candidates who recognized the need of an identity for finding \(\cos 2A\) given \(\cos A\) seldom chose the most appropriate of the three and even when they did often used it incorrectly with expressions such as \(2{\cos ^2}\frac{1}{9} - 1\) .

