| Date | May 2014 | Marks available | 3 | Reference code | 14M.1.sl.TZ2.1 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows a right-angled triangle, \(\rm{ABC}\), where \(\sin \rm{A} = \frac{5}{{13}}\).
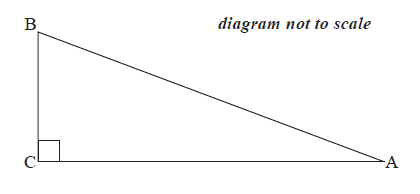
Show that \(\cos A = \frac{{12}}{{13}}\).
Find \(\cos 2A\).
Markscheme
METHOD 1
approach involving Pythagoras’ theorem (M1)
eg \({5^2} + {x^2} = {13^2}\), labelling correct sides on triangle
finding third side is 12 (may be seen on diagram) A1
\(\cos A = \frac{{12}}{{13}}\) AG N0
METHOD 2
approach involving \({\sin ^2}\theta + {\cos ^2}\theta = 1\) (M1)
eg \({\left( {\frac{5}{{13}}} \right)^2} + {\cos ^2}\theta = 1,{\text{ }}{x^2} + \frac{{25}}{{169}} = 1\)
correct working A1
eg \({\cos ^2}\theta = \frac{{144}}{{169}}\)
\(\cos A = \frac{{12}}{{13}}\) AG N0
[2 marks]
correct substitution into \(\cos 2\theta \) (A1)
eg \(1 - 2{\left( {\frac{5}{{13}}} \right)^2},{\text{ }}2{\left( {\frac{{12}}{{13}}} \right)^2} - 1,{\text{ }}{\left( {\frac{{12}}{{13}}} \right)^2} - {\left( {\frac{5}{{13}}} \right)^2}\)
correct working (A1)
eg \(1 - \frac{{50}}{{169}},{\text{ }}\frac{{288}}{{169}} - 1,{\text{ }}\frac{{144}}{{169}} - \frac{{25}}{{169}}\)
\(\cos 2A = \frac{{119}}{{169}}\) A1 N2
[3 marks]

