| Date | May 2008 | Marks available | 2 | Reference code | 08M.2.sl.TZ1.1 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
In a school with 125 girls, each student is tested to see how many sit-up exercises (sit-ups) she can do in one minute. The results are given in the table below.
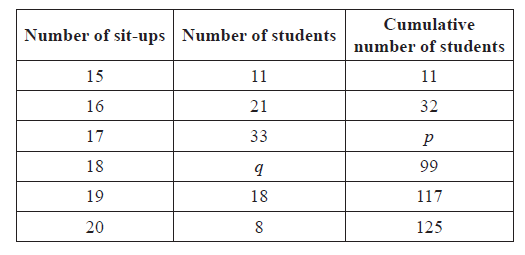
(i) Write down the value of p.
(ii) Find the value of q.
Find the median number of sit-ups.
Find the mean number of sit-ups.
Markscheme
(i) \(p = 65\) A1 N1
(ii) for evidence of using sum is 125 (or \(99 - p\) ) (M1)
\(q = 34\) A1 N2
[3 marks]
evidence of median position (M1)
e.g. 63rd student, \(\frac{{125}}{2}\)
median is 17 (sit-ups) A1 N2
[2 marks]
evidence of substituting into \(\frac{{\sum {fx} }}{{125}}\) (M1)
e.g. \(\frac{{15(11) + 16(21) + 17(33) + 18(34) + 19(18) + 20(8)}}{{125}}\) , \(\frac{{2176}}{{125}}\)
mean \(= 17.4\) A1 N2
[2 marks]
Examiners report
Part (a) of this question was well done.
Finding the median seemed to be the most difficult for the candidates. Most had the idea that it was in the middle but did not know how to find the value.
When calculating the mean, many ignored the frequencies.

