| Date | May 2014 | Marks available | 4 | Reference code | 14M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Show that | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = \frac{{2x}}{{{x^2} + 5}}\).
Use the quotient rule to show that \(f'(x) = \frac{{10 - 2{x^2}}}{{{{({x^2} + 5)}^2}}}\).
Find \(\int {\frac{{2x}}{{{x^2} + 5}}{\text{d}}x} \).
The following diagram shows part of the graph of \(f\).
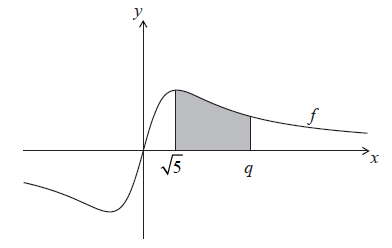
The shaded region is enclosed by the graph of \(f\), the \(x\)-axis, and the lines \(x = \sqrt 5 \) and \(x = q\). This region has an area of \(\ln 7\). Find the value of \(q\).
Markscheme
derivative of \(2x\) is \(2\) (must be seen in quotient rule) (A1)
derivative of \({x^2} + 5\) is \(2x\) (must be seen in quotient rule) (A1)
correct substitution into quotient rule A1
eg \(\frac{{({x^2} + 5)(2) - (2x)(2x)}}{{{{({x^2} + 5)}^2}}},{\text{ }}\frac{{2({x^2} + 5) - 4{x^2}}}{{{{({x^2} + 5)}^2}}}\)
correct working which clearly leads to given answer A1
eg \(\frac{{2{x^2} + 10 - 4{x^2}}}{{{{({x^2} + 5)}^2}}},{\text{ }}\frac{{2{x^2} + 10 - 4{x^2}}}{{{x^4} + 10{x^2} + 25}}\)
\(f'(x) = \frac{{10 - 2{x^2}}}{{{{({x^2} + 5)}^2}}}\) AG N0
[4 marks]
valid approach using substitution or inspection (M1)
eg \(u = {x^2} + 5,{\text{ d}}u = 2x{\text{d}}x,{\text{ }}\frac{1}{2}\ln ({x^2} + 5)\)
\(\int {\frac{{2x}}{{{x^2} + 5}}{\text{d}}x = \int {\frac{1}{u}{\text{d}}u} } \) (A1)
\(\int {\frac{1}{u}{\text{d}}u = \ln u + c} \) (A1)
\(\ln ({x^2} + 5) + c\) A1 N4
[4 marks]
correct expression for area (A1)
eg \(\left[ {\ln \left( {{x^2} + 5} \right)} \right]_{\sqrt 5 }^q,{\text{ }}\int\limits_{\sqrt 5 }^q {\frac{{2x}}{{{x^2} + 5}}{\text{d}}x} \)
substituting limits into their integrated function and subtracting (in either order) (M1)
eg \(\ln ({q^2} + 5) - \ln \left( {{{\sqrt 5 }^2} + 5} \right)\)
correct working (A1)
eg \(\ln \left( {{q^2} + 5} \right) - \ln 10,{\text{ }}\ln \frac{{{q^2} + 5}}{{10}}\)
equating their expression to \(\ln 7\) (seen anywhere) (M1)
eg \(\ln \left( {{q^2} + 5} \right) - \ln 10 = \ln 7,{\text{ }}\ln \frac{{{q^2} + 5}}{{10}} = \ln 7,{\text{ }}\ln ({q^2} + 5) = \ln 7 + \ln 10\)
correct equation without logs (A1)
eg \(\frac{{{q^2} + 5}}{{10}} = 7,{\text{ }}{q^2} + 5 = 70\)
\({q^2} = 65\) (A1)
\(q = \sqrt {65} \) A1 N3
Note: Award A0 for \(q = \pm \sqrt {65} \).
[7 marks]

