| Date | May 2010 | Marks available | 4 | Reference code | 10M.2.sl.TZ1.3 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Sketch | Question number | 3 | Adapted from | N/A |
Question
Let \(f(x) = x\cos x\) , for \(0 \le x \le 6\) .
Find \(f'(x)\) .
On the grid below, sketch the graph of \(y = f'(x)\) .
Markscheme
evidence of choosing the product rule (M1)
e.g. \(x \times ( - \sin x) + 1 \times \cos x\)
\(f'(x) = \cos x - x\sin x\) A1A1 N3
[3 marks]
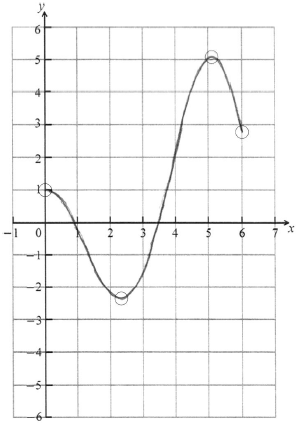A1A1A1A1 N4
Note: Award A1 for correct domain, \(0 \le x \le 6\) with endpoints in circles, A1 for approximately correct shape, A1 for local minimum in circle, A1 for local maximum in circle.
[4 marks]
Examiners report
This problem was well done by most candidates. There were some candidates that struggled to apply the product rule in part (a) and often wrote nonsense like \( - x\sin x = - \sin {x^2}\) .
In part (b), few candidates were able to sketch the function within the required domain and a large number of candidates did not have their calculator in the correct mode.
