| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.sl.TZ2.6 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
The values of the functions \(f\) and \(g\) and their derivatives for \(x = 1\) and \(x = 8\) are shown in the following table.
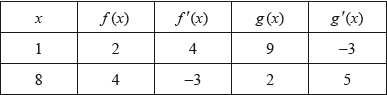
Let \(h(x) = f(x)g(x)\).
Find \(h(1)\).
[2]
a.
Find \(h'(8)\).
[3]
b.
Markscheme
expressing \(h(1)\) as a product of \(f(1)\) and \(g(1)\) (A1)
eg\(\,\,\,\,\,\)\(f(1) \times g(1),{\text{ }}2(9)\)
\(h(1) = 18\) A1 N2
[2 marks]
a.
attempt to use product rule (do not accept \(h’ = f' \times g’\)) (M1)
eg\(\,\,\,\,\,\)\(h’ = fg' + gf',{\text{ }}h'(8) = f'(8)g(8) + g’(8)f(8)\)
correct substitution of values into product rule (A1)
eg\(\,\,\,\,\,\)\(h’(8) = 4(5) + 2( - 3),{\text{ }} - 6 + 20\)
\(h’(8) = 14\) A1 N2
[3 marks]
b.
Examiners report
[N/A]
a.
[N/A]
b.
