On this page you can find examination questions from the topic of geometry and trigonometry
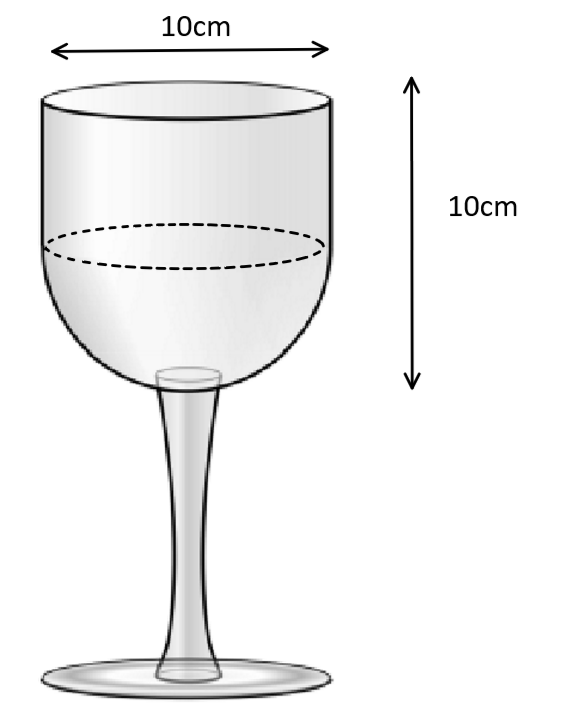


A glass is made up of a hemisphere and a cone.
Find the volume of the glass.
Give your answer to 3 significant figures
Hint
The radius of the cone and the hemisphere are both 5cm
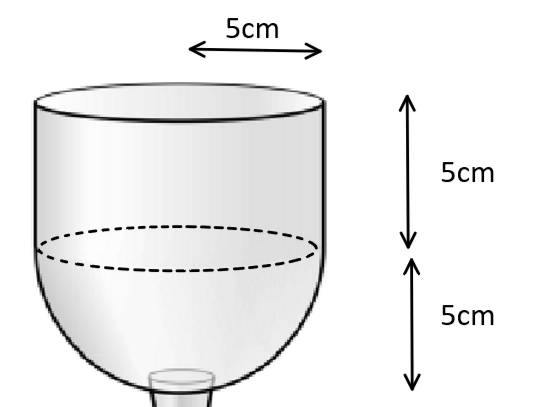
Full Solution
 The radius of the cone and the hemisphere are both 5cm
The radius of the cone and the hemisphere are both 5cm
Volume of cone,
\(\large V_{cone}=\pi r^2h\\ \large V_{cone}=\pi \times5^2\times 5\\ \large V_{cone}=125\pi \)
Volume of hemisphere,
\(\large V_{hemisphere}=2\pi r^2\\ \large V_{hemisphere}=2\times \pi \times 5^2\\ \large V_{hemisphere}=50\pi\)
Total Volume\(\large=125\pi+50\pi\\ \large=175\pi\\ \large\approx549.779...cm^3\\ \large\approx550cm^3\)




The total surface area of a hemisphere is 1360 cm²
Find the radius.
Give your answer to 3 significant figures.
Hint
The surface of a hemisphere is made of two parts
- the curved surface
- the circular base
Full Solution
The surface area of a hemisphere,
\(\large A=\pi r^2+\pi r^2\\ \large A=3\pi r^2\\ \large 1360=3\pi r^2\\ \large r^2=\frac{1360}{3\pi}\\ \large r=\sqrt{\frac{1360}{3\pi}}\\ \large r\approx12.0125...\\ \large r\approx12.0cm \)


a) A sphere has a radius of 10cm. Find the volume, giving your answer in terms of \(\large \pi\).
b) A cone has the same volume and the same radius as the sphere. Find the height of the cone.
c) Another sphere and cone have the same volume and the same radius, r. Find an equation for the height of the cone, h in terms of r.
Hint
c) Solve \(\large \frac{4}{3}\pi r^3=\frac{1}{3}\pi r^2h\\\)
Full Solution
a)
\(\large V=\frac{4}{3}\pi r^3\\ \large V=\frac{4}{3}\pi \times10^3\\ \large V=\frac{4000}{3}\pi \ cm^3\)
b)
\(\large V=\frac{1}{3}\pi r^2h\\ \large \frac{4000}{3}\pi=\frac{1}{3}\pi \times 10^2\times h\\ \large h=40\ cm\)
c)
\(\large \frac{4}{3}\pi r^3=\frac{1}{3}\pi r^2h\\ \large \frac{4}{\rlap{/}3}\rlap{/}\pi r^3=\frac{1}{\rlap{/}3}\rlap{/}\pi r^2h\\ \large 4r^3=r^2h\\ \large 4r=h\\ \large h=4r\)


Three metal spheres have radii 1cm, 6cm and 8cm.
The spheres are melted down and made into one bigger sphere.
What is the radius of the single sphere?

Hint
Full Solution
The volume of a sphere is given by \(\large V=\frac{4}{3}\pi r^3\)
The Volume of the three spheres is
\(\large V=\frac{4}{3}\pi \times1^3+\frac{4}{3}\pi \times 6^3+\frac{4}{3}\pi \times 8^3\\ \large V=\frac{4}{3}\pi \times(1^3+6^3+8^3)\\ \large V=\frac{4}{3}\pi \times(729)\\ \)
The large sphere has the same volume as these three spheres
\(\large \frac{4}{3}\pi \times R^3=\frac{4}{3}\pi \times(729)\\ \large R^3=729\\ \large R=9\ cm \)


A cylindrical metal bar with height 12cm and diameter 12cm is melted down and made into spheres of diameter 3cm.
How many spheres will it make?
Hint
Full Solution
The volume of the cylindrical bar is
\(\large V=\frac{1}{3}\pi\times 6^2\times12\\ \large V=144\pi \)
The volume of one of the spheres is
\(\large V=\frac{4}{3}\pi\times 1.5^3\\ \large V=4.5\pi \)
Therefore, the number of spheres is \(\large \frac{144\pi}{4.5\pi}\)
\(\large 32\) spheres
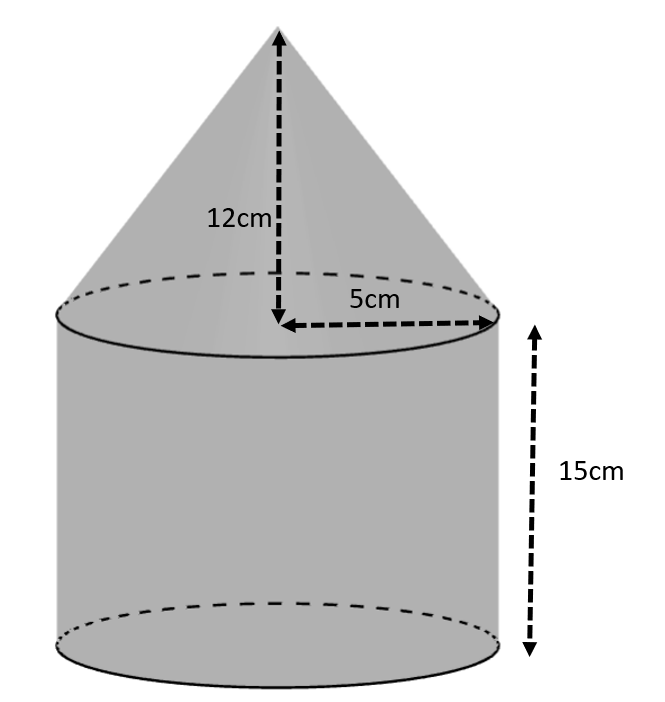


A solid is made up of a cone and a cylinder.
The radius is 5cm, the height of the cone is 12cm and the height of the cylinder is 15cm.
Show that the total surface area of the solid is \(\large 240\pi\)
Hint
There are three surfaces to find: the curved surface of the cone, the curved surface of the cylinder and the circular base.
To find the curved surface area of the cone, you need to find the slant height. Use Pythagoras' Theorem.
Full Solution
 We need to find the slant height of the cone:
We need to find the slant height of the cone:
\(\large l^2=5^2+12^2\\ \large l^2=169\\ \large l=13\)
The surface area of the cone is
\(\large A_{cone}=\pi rl\\ \large A_{cone}=\pi\times5\times 13\\ \large A_{cone}=65\pi\)
The surface area of the cylinder is
\(\large A_{cylinder}=2\pi rh\\ \large A_{cylinder}=2\pi \times 5\times 15\\ \large A_{cylinder}=150\pi\)
The area of the base is
\(\large A_{base}=\pi r^2\\ \large A_{base}=\pi \times 5^2\\ \large A_{base}=25\pi \)
The total surface area is
\(\large =65\pi+150\pi+25\pi\\ \large=240\pi\)



The following diagram shows a circle with centre O and radius 12cm. A and B lie on the circumference of the circle and \(\large AÔB=50°\)
a) Find the area of the minor sector OAB
b) Find the area of the triangle AOB
c) Hence, find the area of the shaded segment
Hint
Full Solution
a) The angle is given in degrees
\(\large A_{sector}= \frac{\theta}{360}\pi r^2\\ \large A_{sector}= \frac{50}{360}\pi \times 12^2\\ \large A_{sector}=20\pi\\ \large A_{sector}\approx62.831...\\ \large A_{sector}\approx62.8cm^2 \)
b) The area of the triangle is
\(\large A_{triangle}= \frac{1}{2} ab \sin C\\ \large A_{triangle}= \frac{1}{2} r^2 \sin \theta\\ \large A_{triangle}= \frac{1}{2} \times12^2 \times\sin 50°\\ \large A_{triangle}\approx55.155...\\ \large A_{triangle}\approx55.2cm^2 \)
c) The area of the segment = area of sector - area of triangle
Be careful to use a higher degree of accuracy for parts a) and b) to give the final answer correct to 3 s.f.
\(\large A_{sector}\approx62.831...-55.155...\\ \large A_{sector}\approx7.68cm^2\)



The following diagram shows a circle with centre O and radius r cm
The area of the shaded sector OAB is \(\large \frac{40\pi}{3}\) cm²
The length of the minor arc AB is \(\large \frac{10\pi}{3}\) cm
a) Find the radius of the circle
b) Find the angle \(\large \theta\) , in radians
Hint
Write an equation for the arc length and another equation for the sector area.
Full Solution
a) The area of the shaded sector OAB is \(\large \frac{40\pi}{3}\) cm²
\(\large A=\frac{1}{2}r^2\theta\\ \large \frac{40\pi}{3}=\frac{1}{2}r^2\theta\\\)
The length of the minor arc AB is \(\large \frac{10\pi}{3}\) cm
\(\large l=r\theta\\ \large \frac{10\pi}{3}=r\theta\)
Let's solve these equations by substituting for \(\large r\theta\) into the area equation
\(\large \frac{1}{2}r^2\theta=\frac{40\pi}{3}\\\)
\(\large \frac{1}{2}r\times r\theta=\frac{40\pi}{3}\\\)
\(\large \frac{1}{2}r\times \frac{10\pi}{3}=\frac{40\pi}{3}\\\)
\(\large \frac{1}{2}r=4\)
r = 8 cm
We can now find the angle by substituting this value into the length equation
\(\large \frac{10\pi}{3}=8\times\theta\\ \large \theta=\frac{10\pi}{24}\\ \large \theta=\frac{5\pi}{12}\)


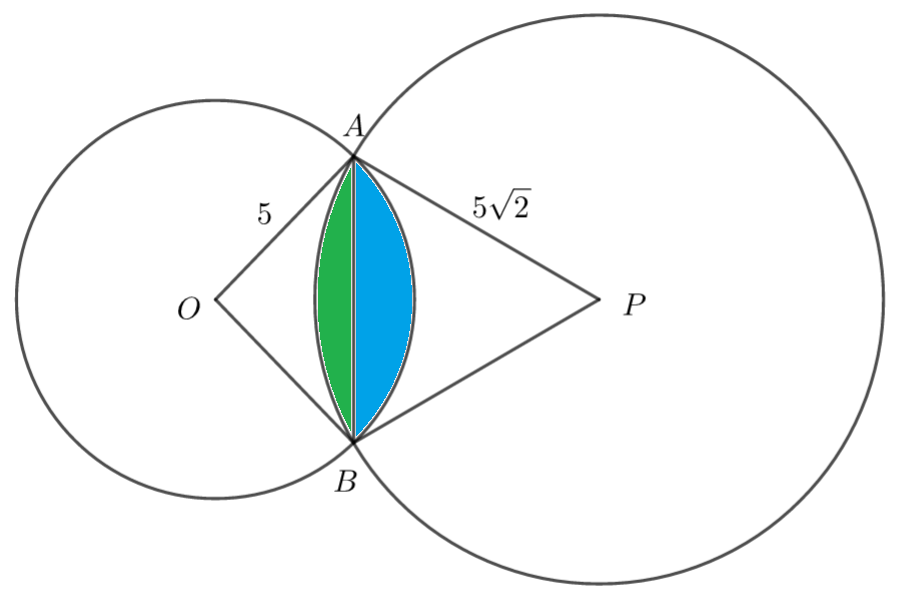
The following diagram shows a circle with centre O and radius 5cm and another circle with centre P and radius r. The two circles overlap meeting at points A and B. \(\large AÔP=45°\) and \(\large A\hat{P}O=30°\)

a) Show that \(\large r=5\sqrt{2}\) cm
b) Hence, show that the shaded area bounded by the two circles is \(\large \frac{25}{12}(7\pi-6-6\sqrt3)\) cm²
Hint
a) You can use the Sine Rule to find r.
Full Solution
a)
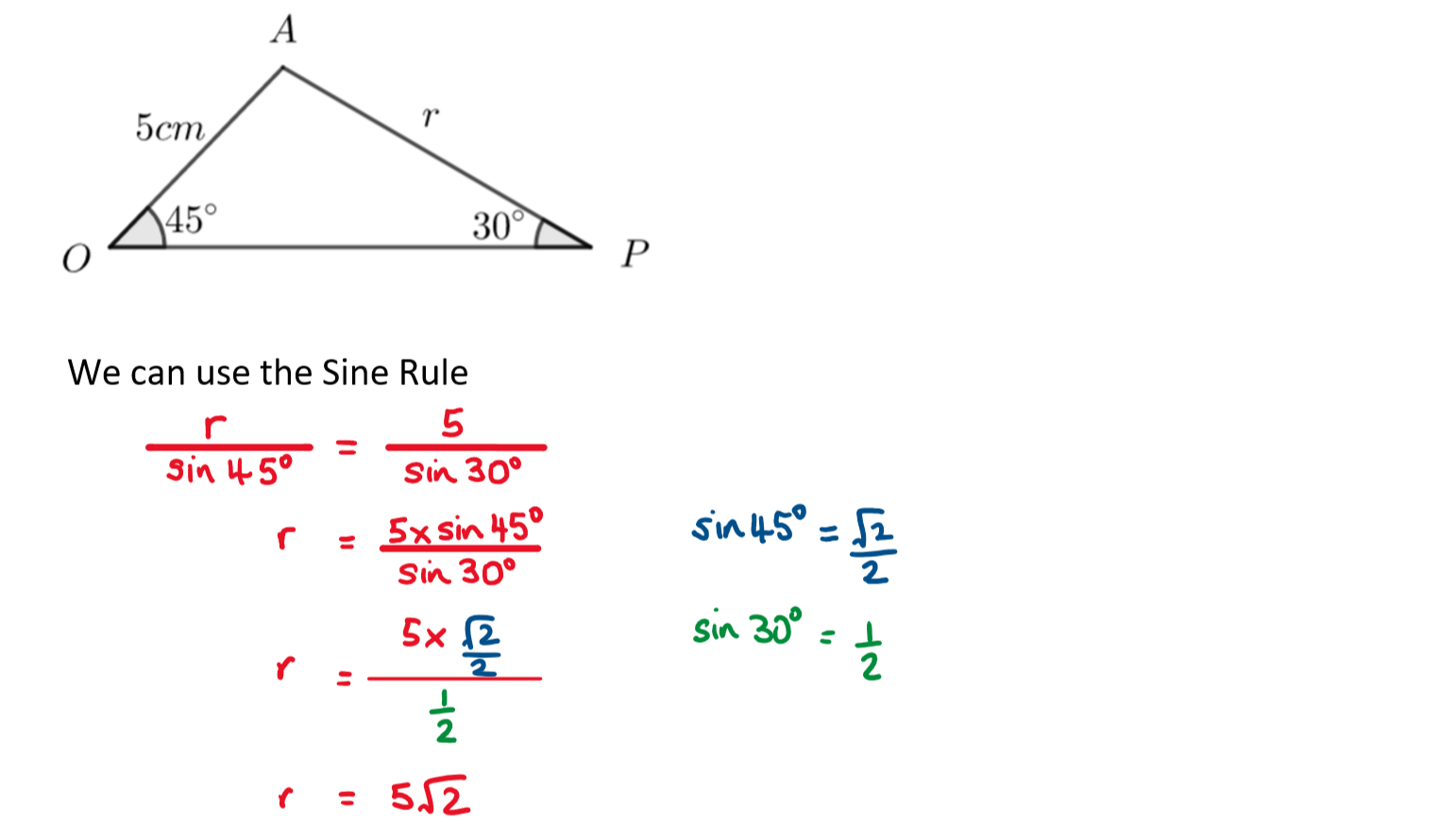
b) Divide the shaded area into two parts.


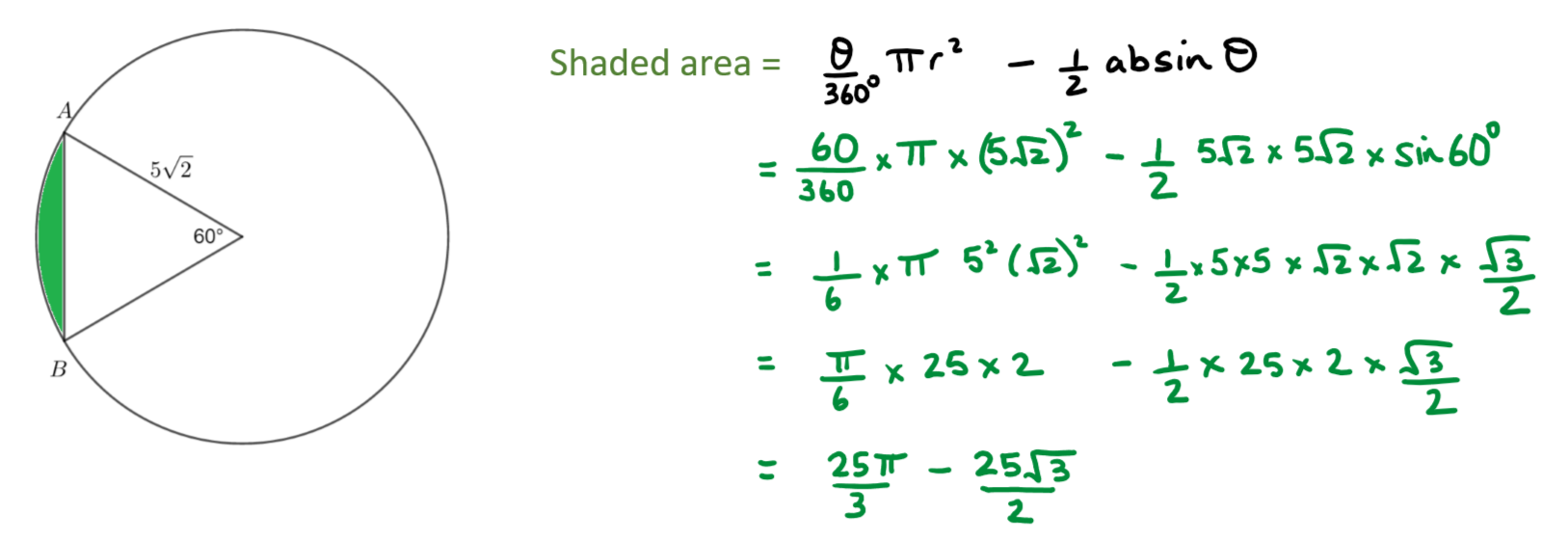



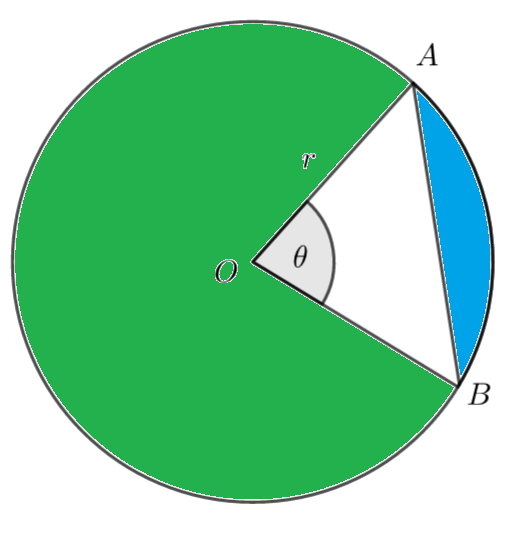
The following diagram shows a circle with centre O and radius r. A and B are points on the circumference of the circle and \(\large A\hat{O} B =\theta\) radians
The area of the green shaded region is three times greater than the area of the blue region.
a) Show that \(\large \sin \theta=\frac{4\theta-2\pi}{3}\)
b) Find the value of \(\large \theta\) , giving your answer correct to 3 significant figures.
Hint
a) The area of the blue segment = area of sector - area of triangle
Full Solution
a)

area of the blue segment = area of sector - area of triangle
\(\large A_{segment}=\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta\)
 The angle subtended by the the green sector is \(\large 2\pi-\theta\)
The angle subtended by the the green sector is \(\large 2\pi-\theta\)
Area of the green sector is
\(\large A_{sector}=\frac{1}{2}r^2(2\pi-\theta)\)
The area of the green sector = three times the area of the blue segment
\(\large \frac{1}{2}r^2(2\pi-\theta)\) = 3 \(\large (\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\theta)\)
\(\large \frac{1}{2}r^2(2\pi-\theta)=\frac{3}{2}r^2(\theta-\sin\theta)\)
\(\large 2\pi-\theta=3(\theta-\sin\theta)\\ \large 2\pi-\theta=3\theta-3\sin\theta\\ \large 3\sin\theta=4\theta-2\pi\\ \large \sin\theta=\frac{4\theta-2\pi}{3}\)
b) We can solve this equation using our graphical equation.You can plot the graphs of \(\large y=\sin\theta\\ \) and \(\large y=\frac{4\theta-2\pi}{3}\) and find the point of intersection
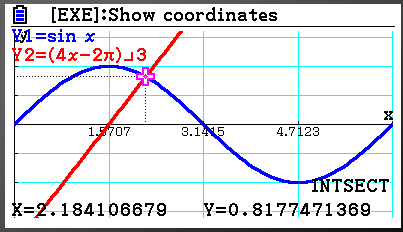
\(\large \theta \approx2.18\)
The diagram looks approaximately like the following
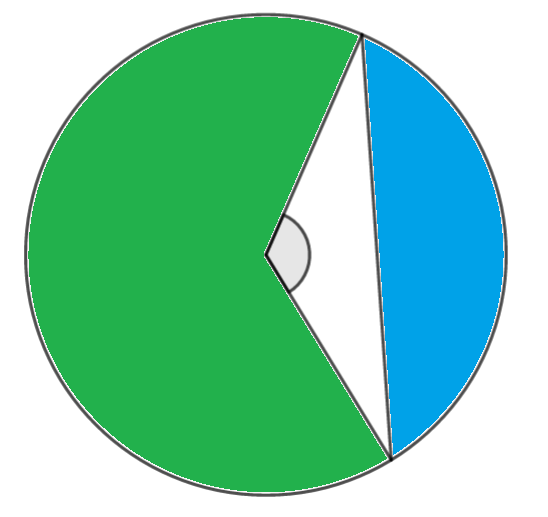



The following diagram shows a circle with centre O and radius r. Points A and B lie on the circumference of the circle and \(\large A\hat{O}B=\theta\) radians. The tangents to the circle A and B intersect at C.
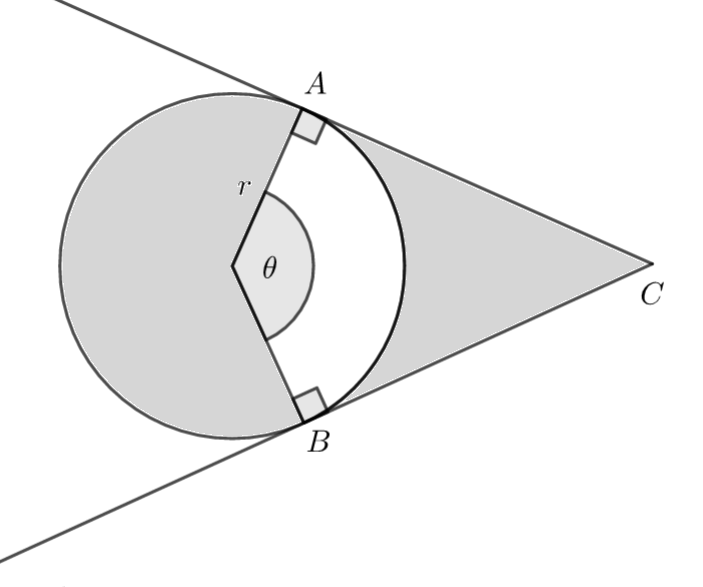
a) Show that \(\large AC=r\tan (\frac{\theta}{2})\)
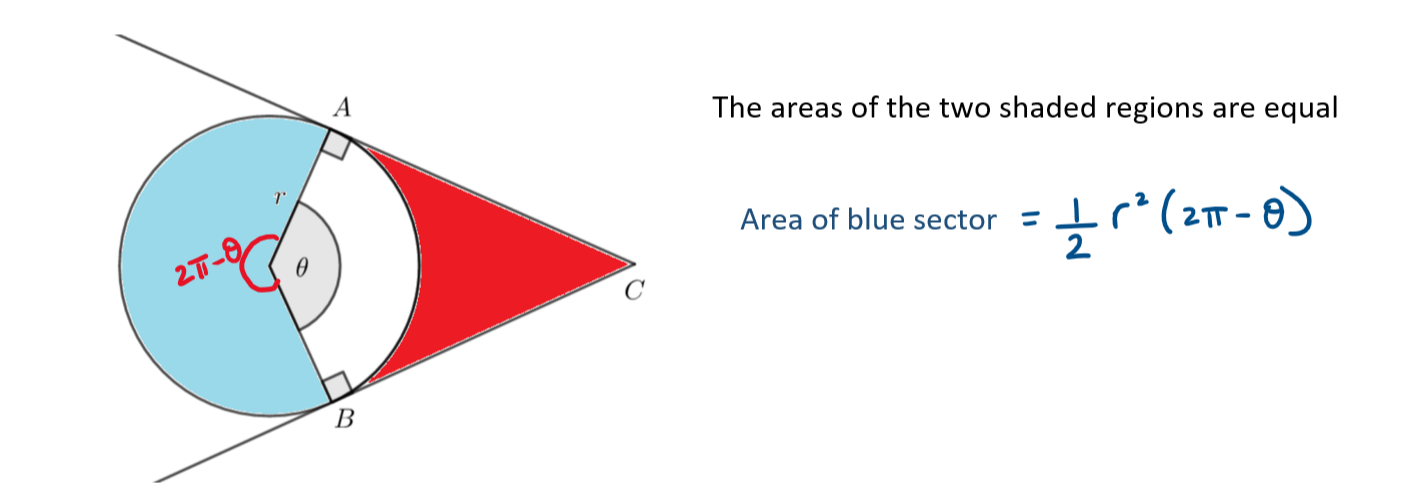
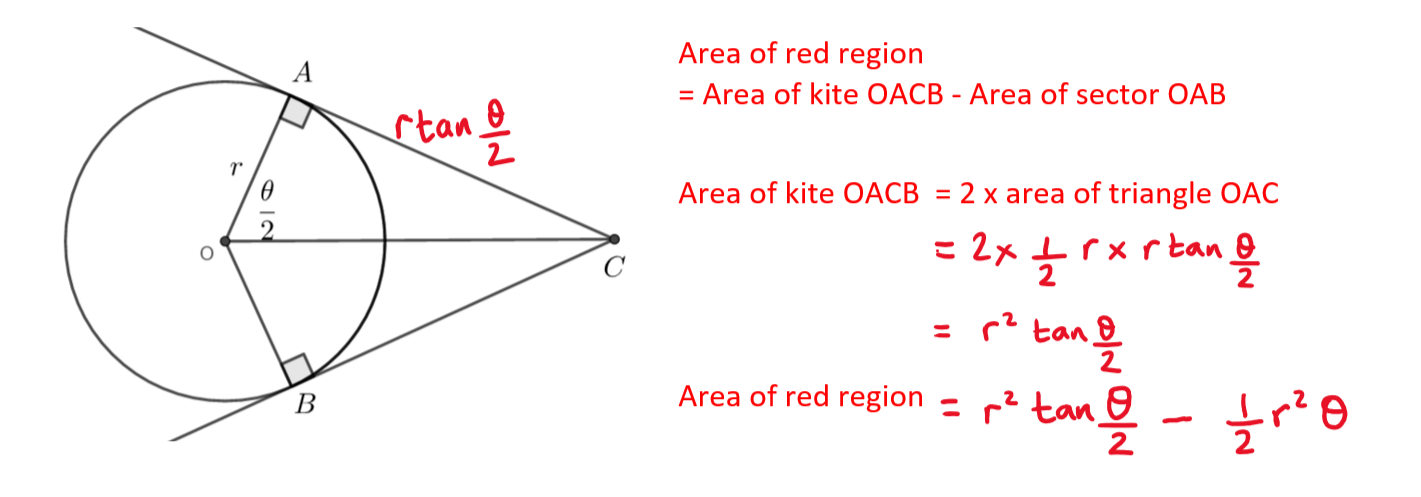
b) Hence, find the value of \(\large \theta\) when the two shaded regions have an equal area.
Hint
b) Area of red region = Area of kite OACB - Area of sector OAB
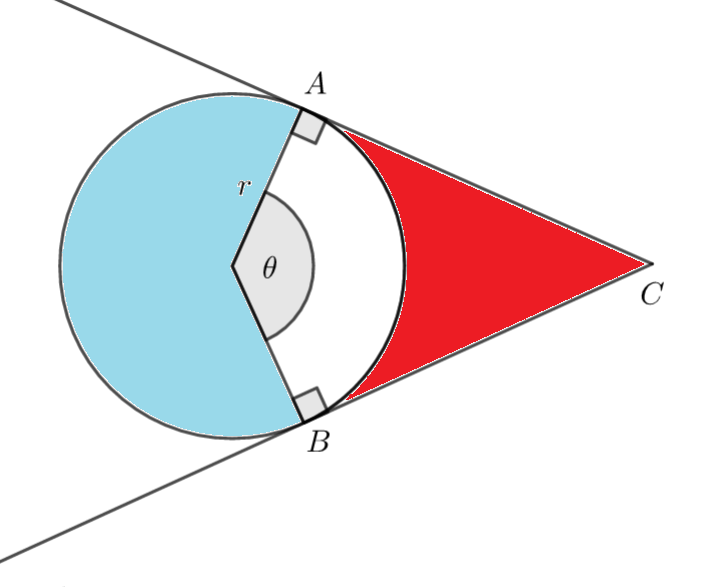
Full Solution
a) Triangle OAC is a right angled triangle, so we can use right-angled triangle trigonometry to work out the length AC (opposite to the angle \(\large\frac{\theta}{2}\)
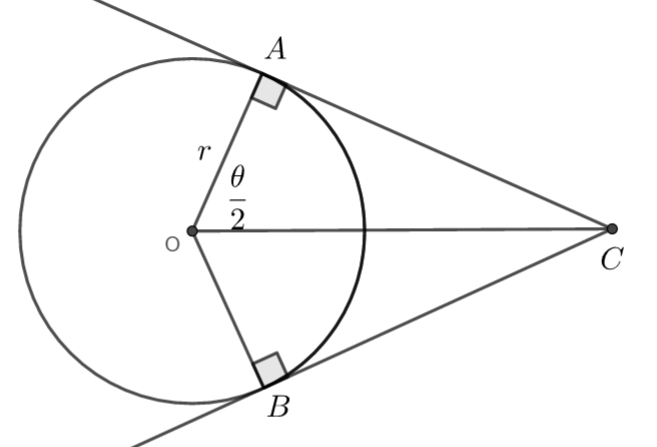
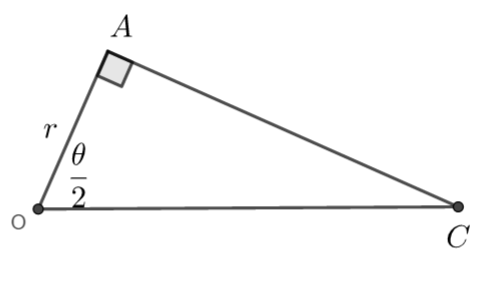
\(\large \tan\frac{\theta}{2}=\frac{AC}{r}\)
\(\large AC=r\tan\frac{\theta}{2}\)
b)



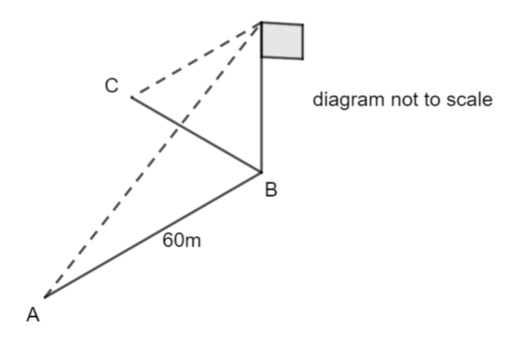
A, B and C are points on horizontal ground.
C is due West of B. A is due South of B. AB = 60m
A flagpole stands vertically at B.
From A, the angle of elevation of the top of the flagpole is 11°.
From B, the angle of elevation of the top of the flagpole is 15°.
Calculate the distance AC giving your answer to 3 significant figures.
Hint
Full Solution
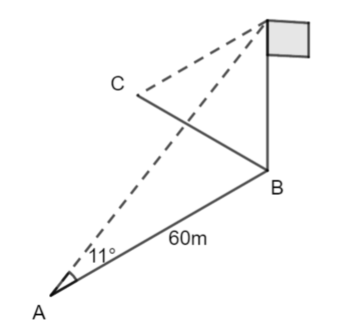 We can find the height of the flagpole
We can find the height of the flagpole
\(\large\tan11°=\frac{h}{60}\\ \large h=60\times\tan11°\\ \large h\approx 11.7\)
use calculator memory to store the exact value of this length
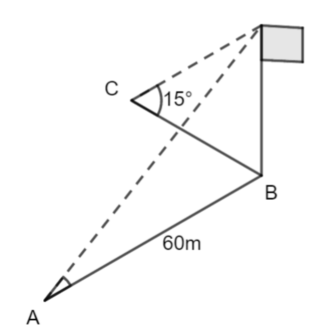 Now we can find the length BC
Now we can find the length BC
\(\large\tan15°=\frac{h}{BC}\\ \large BC=\frac{h}{tan15°}\\ \large BC=\frac{60\times \tan11°}{tan15°}\\\\ \large BC\approx 43.5\)use the exact value of h
use calculator memory to store the exact value of this length
ABC is a right-angled triangle
\(\large AC^2=AB^2+BC^2\\ \large AC^2=60^2+(43.5...)^2\\ \large AC\approx74.1m\)


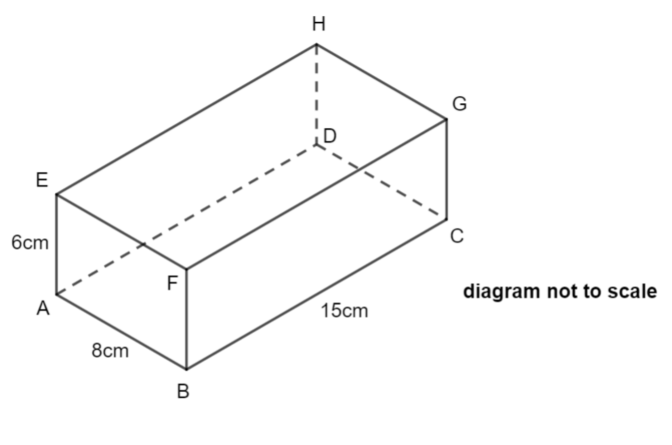
The diagram shows a cuboid ABCDEFGH. AB = 8 cm, AE = 6 cm and BC = 15 cm.
a) Find the length of AC.
Give your answer correct to 3 significant figures
b) Find the size of the angle between the line EC and the plane ABCD.
Give your answer correct to 1 decimal place.
Hint
b) Here is the right-angled triangled you should consider for this question
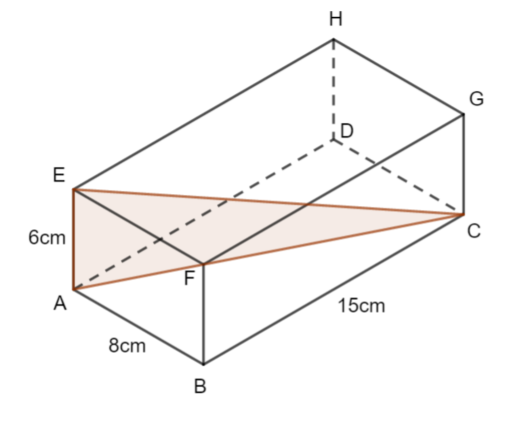
Full Solution
a)
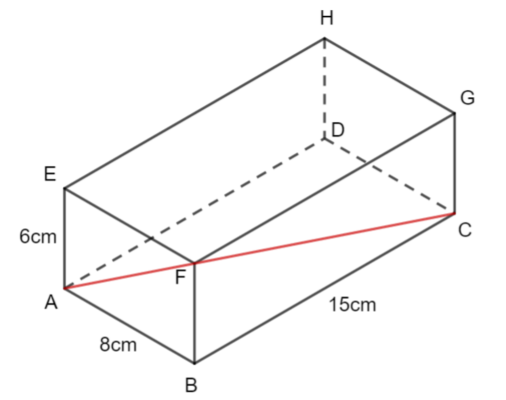
ABC is a right-angled triangle.
Use Pythagoras' Theorem to work out AC.
AC² = 8² + 15²
AC² = 289
AC = 17cm
b)
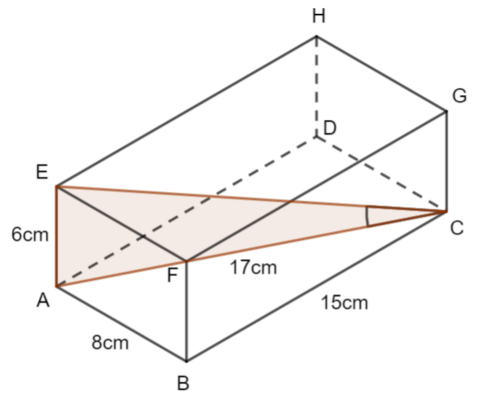 The angle between the line EC and the plane ABCD can be visualised in the diagram.
The angle between the line EC and the plane ABCD can be visualised in the diagram.
EAC is a right-anghled triangle.
We can use trigonometry to work out the angle
\(\large \tan\theta=\frac{6}{17}\\ \large\theta=\tan^{-1}(\frac{6}{17})\\ \large\theta\approx19.4°\)


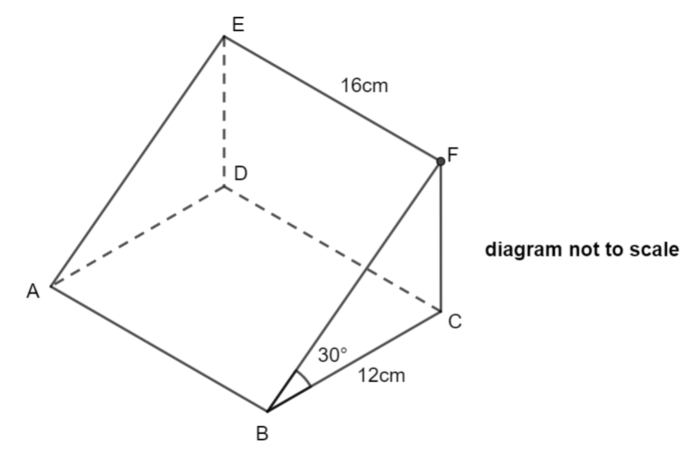
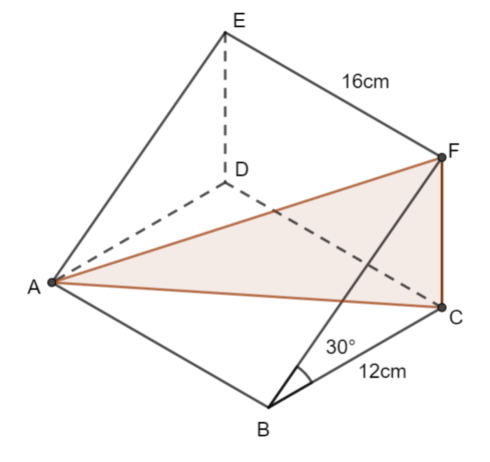
ABCDEF is a prism in which the triangle BCF is the cross section.
BC = 12cm, EF = 16cm, angle CBF = 30° and angle FCB = 90°
The angle AF makes with the plane ABCD is \(\large \theta\).
Show that \(\large \tan\theta=\frac{\sqrt{3}}{5}\)
Hint
The following triangle helps you to see the angle that is required.
Full Solution
We can work out the lengths CF and CA
Use the triangle CBF to work out CF
\(\large \tan30°=\frac{CF}{12} \qquad \qquad \tan30°=\frac{\sqrt{3}}{3}\\ \large \frac{\sqrt{3}}{3}=\frac{CF}{12}\\ \large \frac{12\sqrt{3}}{3}=CF\\ \large CF=4\sqrt{3}\)
Use Pythagoras' Theorem to work out CA
CA² = 12² + 16²
CA² = 400
CA = 20
Now put this information in the diagram
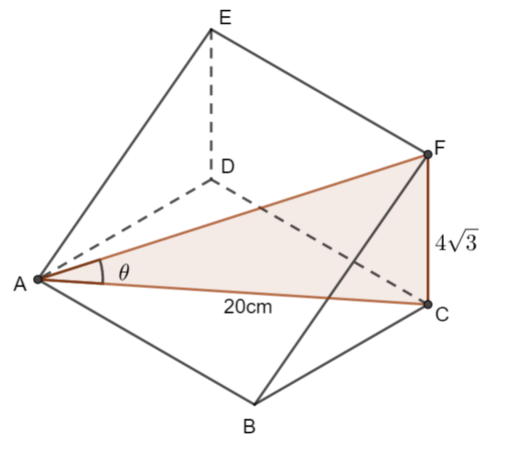
\(\large \tan\theta=\frac{4\sqrt{3}}{20}\\ \large \tan\theta=\frac{\sqrt{3}}{5}\)


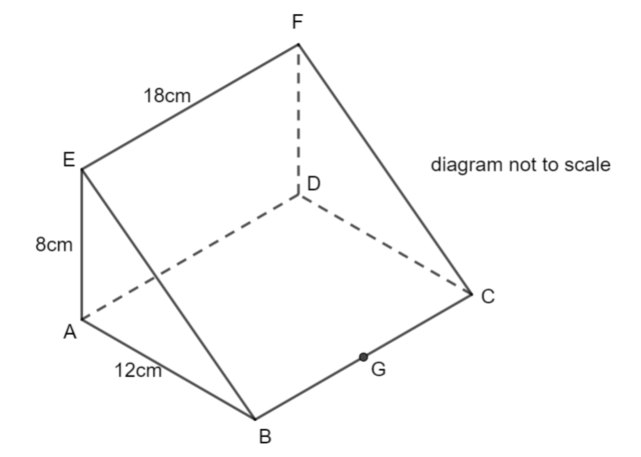
ABCDEFG is a triangular prism.
AB = 12cm, AE = 8cm, EF = 18cm.
Angle BAE = 90°
G is the midpoint of BC.
Calculate the angle between EG and the plane ABCD.
Give your answer correct to 1 decimal place.
Hint
Here is the triangle that contains the angle required
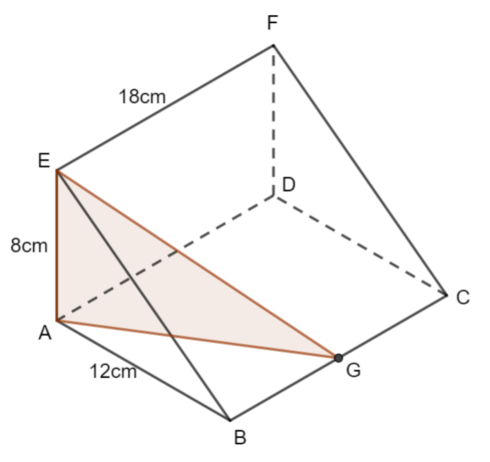
Full Solution
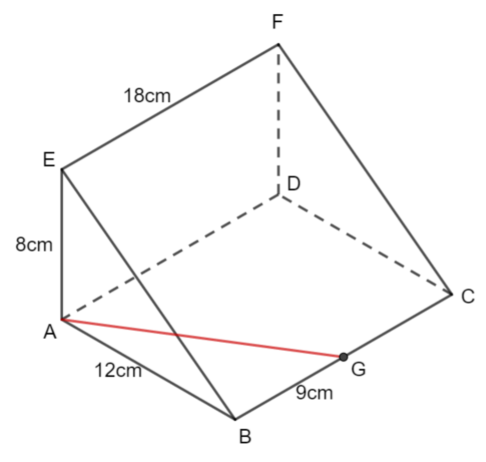 We shoud calculate the length AG using Pythagoras' Theorem.
We shoud calculate the length AG using Pythagoras' Theorem.
G is the midpoint of BC. Therefore BG is 9cm.
AG² = 9² + 12²
AG² = 225
AG = 15
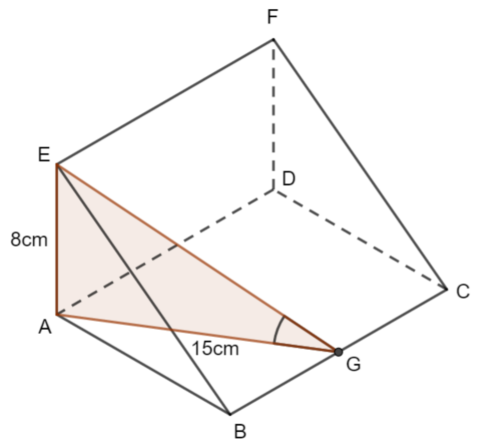 Here is the angle that we are required to find.
Here is the angle that we are required to find.
It is a right-angled triangle.
\(\large \tan\theta =\frac{8}{15}\\ \large\theta=\tan^{-1}(\frac{8}{15})\\ \large\theta\approx24.0°\)


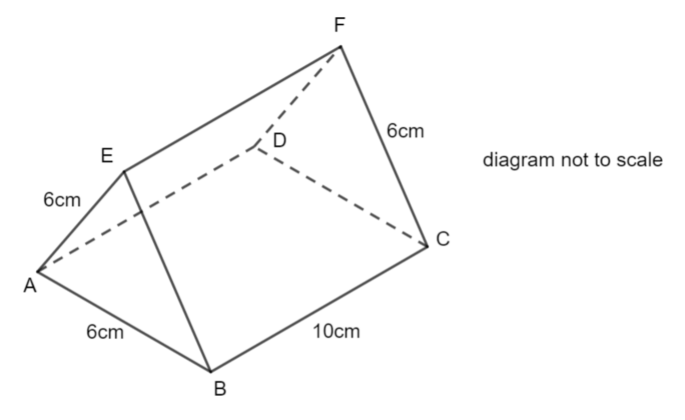
ABCDEF is a prism.
AB = AE = BE = 6cm. BC = 10cm
Calculate
a) the length EC
b) the angle AEC
c) the angle between EC and the plane ABCD
Give lengths to 3 significant figures and angles to 1 decimal place.
Hint
For parts b) and c), the challenge is to visualise the triangles required to find the angles. The question aims to show you that the angles in part b) and c) are not the same!
b)
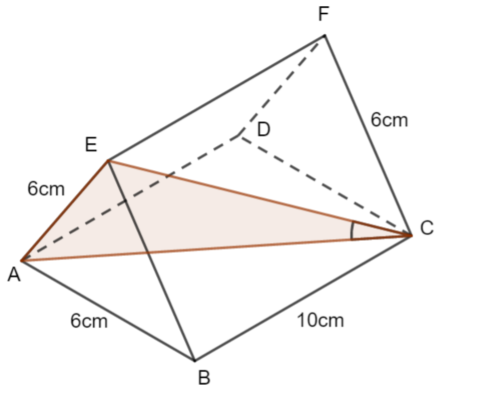
c)
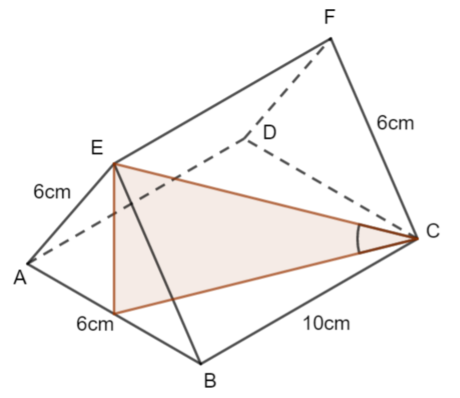
Full Solution
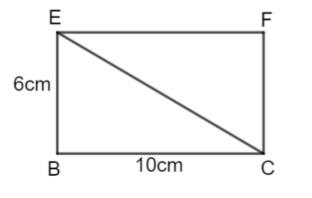 a) WE can find the length EC using Pythagoras' Theorem
a) WE can find the length EC using Pythagoras' Theorem
EC² = 10² + 6²
EC² = 136
\(\large EC = \sqrt{136}\)
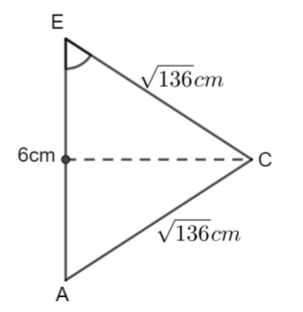 b) The length AC is the same as EC
b) The length AC is the same as EC
We have an isoceles triangle. Use just the top half of the triangle and right-angled trigonometry to find the angle ACE (or you can use the whole triangle and the cosine rule).
\(\large \cos\theta=\frac{3}{\sqrt{136}}\\ \large \theta=\cos^{-1}(\frac{3}{\sqrt{136}})\\ \large \theta\approx75.1°\)
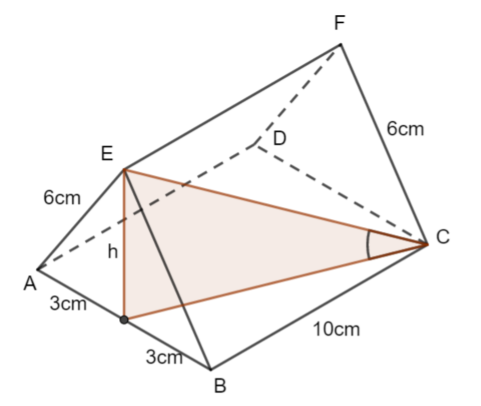 c) The angle between EC and the plane ABCD can be visualised in this diagram.
c) The angle between EC and the plane ABCD can be visualised in this diagram.
We know the length EC =\(\large \sqrt{136}\)
We need to find another legnth in this right-anghled triangle. Find the height of the triangle:
\(\large h^2=6^2-3^2\\ h=\sqrt{27}\)
Let \(\large \alpha\) be the angle between EC and the plane ABCD
\(\large\sin\alpha=\frac{\sqrt{27}}{\sqrt{136}}\\ \large\alpha\approx26.5°\)


The following diagram shows a quadrilateral ABCD.
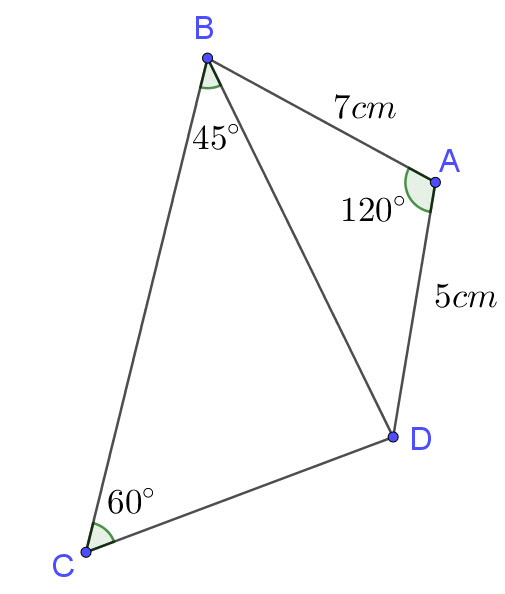
AB = 7cm , AD = 5cm ∠DAB=120° , ∠DBC=45° , ∠BCD=60°
BD = \(\sqrt{a}\)
CD = \(\sqrt{b}\)
\(a,b \in \mathbb{Z}\)
Find a and b
Hint
Full Solution
Print from here


The following diagram shows a quadrilateral ABCD.
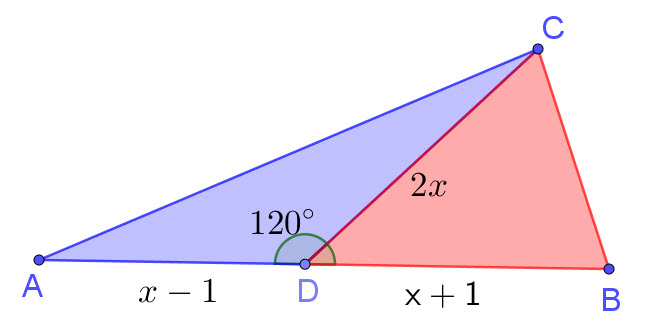
AD = x – 1 , BD = x + 1 , DC = 2x and \(\angle CDA\) = 120°
The sum of the area of triangle ADC and triangle BDC is \(4 \sqrt{3}\)
Find x
Hint
Full Solution
Print from here


In a triangle ABC, AB = 8cm, BC = a, AC = b and \(\angle BAC\) = 30°
a) Show that \(b^2-8\sqrt{3}b+64-a^2=0\)
b) Hence find the possible values of a (in cm) for which the triangle has two possible solutions.
Hint
a) Use the cosine rule.
The following applet might help you visualise the triangle. Drag the slider to see the different possible values that a can take
Full Solution
Print from here

Given that \(cosx=-\frac{\sqrt{7}}{3}\) and \(\frac{\pi}{2}\le x\le \pi\) , find the possible values of sinx and tanx
Hint
Draw a circle.
Full Solution
Print from here

If \(tanx=\frac{12}{5}\) and \(\pi\le x\le \frac{3\pi}{2}\) , find the value of cosx
Hint
Draw a circle.
Full Solution
Print from here


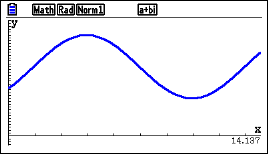
The height h of water, in metres, in a habour is modelled by the function \(\large h(t)=5.5\sin(0.5(t-1.5))+12\) where t is time after midday in hours.
a) Find the initial height of the water.
b) At what time is it when the water reaches this height again?
c) Find the maximum height of the water.
d) How much time is there in between the first and second time that the water at 16 metres?
Give heights to 3 significant figures and times to the nearest minute
Hint
This question gets you to use your calculator to solve problems.
Ensure that your calculator is in radian mode.
Adjust the view window so that you get a good view of the graph
Full Solution
a) 8.25 metres

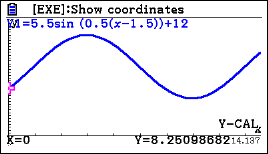
b) 21:17 or 9.17 pm
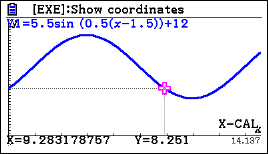 0.283x60 = 17 minutes
0.283x60 = 17 minutes
c) 4.64 meters
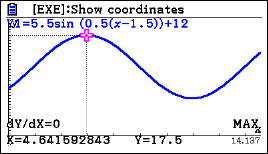
d) 3 hours 2 mins
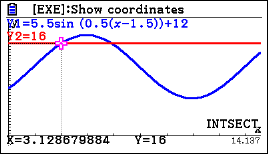

6.155 - 3.129 = 3.026
0.026 x 60 = 2 mins


The following diagram shows a Ferris wheel.
The height, h metres of a seat above ground after t minutes is given by \(\large h(t)=a\ \cos(bt)+c\) , where a, b and c \(\large \in \mathbf{R}\)
The following graph shows the height of the seat.
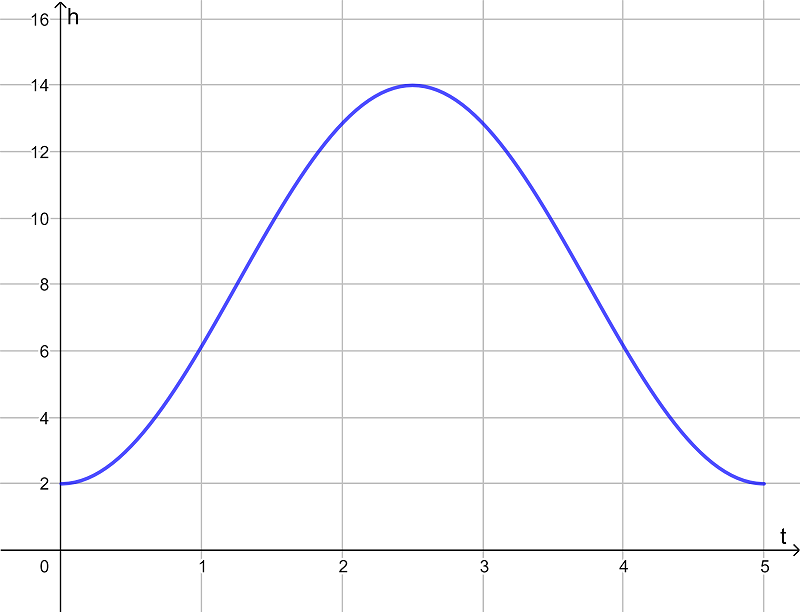
Find the values of a, b and c
Hint
amplitude is |a|
vertical shift = c
Full Solution
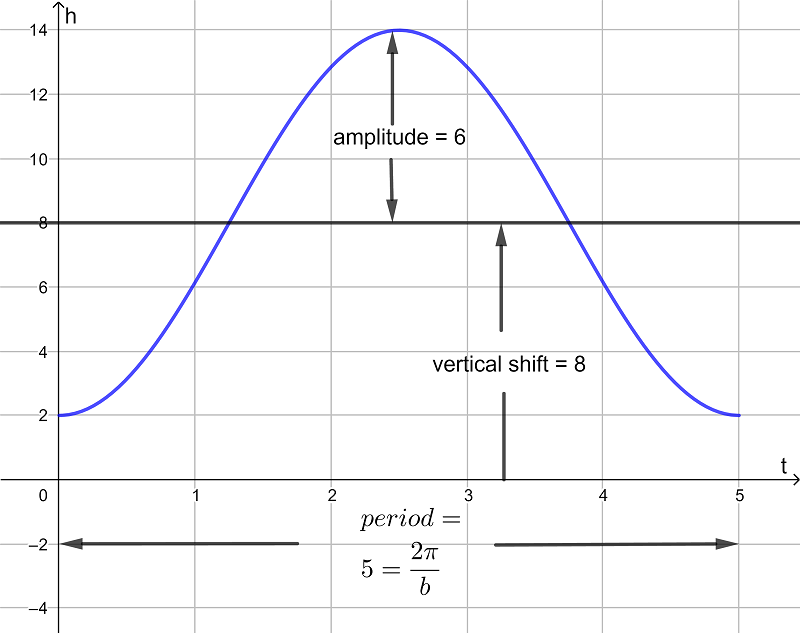
amplitude is |a| = 6 , a = -6
vertical shift = c = 8


Consider a function f, such that \(\large f(x) = 5.6\cos(\frac{\pi}{a}(x-1))+b\) , \(\large 0\le x\le 15\), \(\large a,b\in \mathbf{R}\)
The function f has a local maximum at the point (1 , 8.8) and a local minimum at the point (10 , -2.4)
a) Find the period of the function
b) Hence, find the value of a.
c) Find the value of b.
Hint
For \(\large f(x)=a \cos(b(x+c))+d\)
period = \(\large \frac{2\pi}{b}\)
Full Solution
a) period = 18

b) period = \(\large \frac{2\pi}{\frac{\pi}{a}}\)
\(\large \frac{2\pi}{\frac{\pi}{a}}=18\\ \large 2a = 18\\ \large a = 9\)
c) Use (1 , 8.8)
\(\large5.6\cos(\frac{\pi}{9}(1-1))+b=8.8\\ \large5.6\cos(0)+b=8.8\\ \large5.6+b=8.8\\ \large b=3.2\)


Consider a function f, such that \(\large f(x) = a\sin(\frac{\pi}{15}(x+2))+b\) , \(\large a,b\in \mathbf{R}\)
The function f has passes through the points (10.5 , 5.5) and (15.5 , 2.5)
Find the value of a and the value of b
Hint
This will give you two equations for the unknowns a and b.
Solve these equations
Full Solution
\(\large f(x) = a\cos(\frac{\pi}{15}(x+2))+b\)
(10.5 , 5.5)
\(\large a\sin(\frac{\pi}{15}(10.5+2))+b=5.5\\ \large a\sin(\frac{12.5}{15}\pi)+b=5.5\\ \large a\sin(\frac{25}{30}\pi)+b=5.5\\ \large a\sin(\frac{5}{6}\pi)+b=5.5\\ \large a(0.5)+b=5.5\\ \large a+2b=11\)
(15.5 , 2.5)
\(\large a\sin(\frac{\pi}{15}(15.5+2))+b=2.5\\ \large a\sin(\frac{17.5}{15}\pi)+b=2.5\\ \large a\sin(\frac{35}{30}\pi)+b=2.5\\ \large a\sin(\frac{7}{6}\pi)+b=2.5\\ \large a(-0.5)+b=2.5\\ \large -a+2b=5\)
a + 2b = 11
-a + 2b = 5
4b = 16
b = 4
a= 3


The following diagram shows a ball attached to the end of a spring.
The height, h, in mtres of the ball above the ground t seconds after being released can be modelled by the function
\(\large h(t)=a\cos(\frac{\pi}{b}t)+c\) , \(\large a,b, c\in \mathbf{R}\)
The ball is release from an initial height of 4 metres.
After \(\large \frac{4}{3}\) seconds, the ball is at a height of 1.6 metres.
It takes the ball 4 seconds to return to its initial height.
Find the values of a, b and c.
Hint
If it takes 4 seconds to return to the initial height, then the period = 4
Full Solution
If it takes 4 seconds to return to the initial height, then the period = 4
\(\large \frac{2\pi}{\frac{\pi}{b}}=4\\ \large b=2\)
\(\large h(t)=a\cos(\frac{\pi}{2}t)+c\)
When t = 0, h = 4
\(\large a\cos(0)+c=4\\ \large a+c=4\)
When t = \(\large \frac{4}{3}\), h = 1.6
\(\large a\cos(\frac{\pi}{2}(\frac{4}{3}))+c=1.6\\ \large a\cos(\frac{2\pi}{3})+c=1.6\\ \large a(-0.5)+c=1.6\\ \large -a+2c=3.2\)
a + c = 4
-a + 2c = 3.2
3c = 7.2
c = 2.4
a = 1.6


a) Show that the equation \(\large 2 \sin^2x=3 \cos x\) may be written in the form
\(\large 2 \cos^2x+3 \cos x-2=0\)
b) Hence, solve \(\large 2 \sin^2x=3 \cos x\) , for \(\large 0\le x\le2\pi\)
Hint
a) Use \(\large \cos^2 x+\sin ^2x\equiv1\)
b) Use the answer from part a). This is a quadratic equation.
Don't forget that \(\large \cos^2 x\) means \(\large (\cos x)^2\)
Full Solution
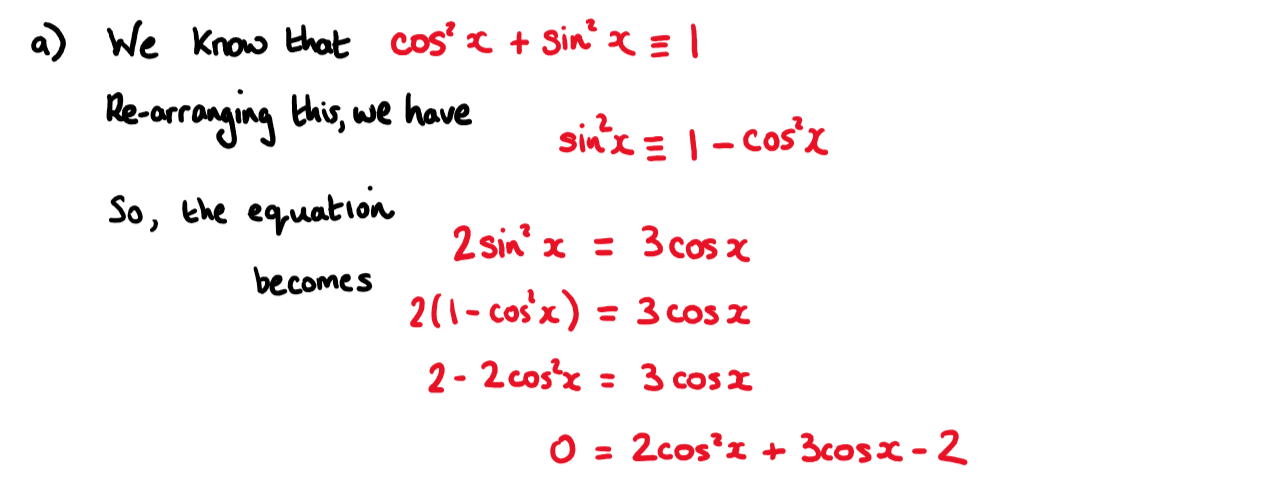

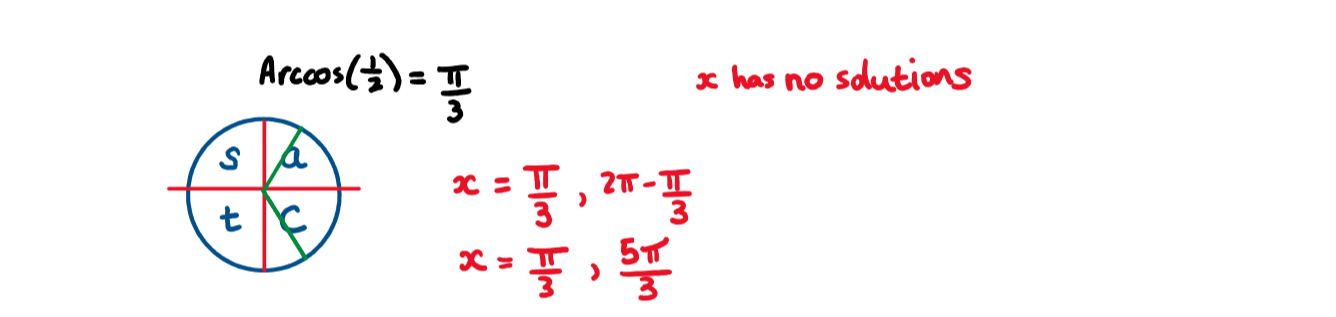



Given that \(x=\frac{2}{cos\theta}\) and \(y=3tan\theta\)
show that \(\frac{x^2}{4}-\frac{y^2}{9}=1\)
Hint
Full Solution
Print from here


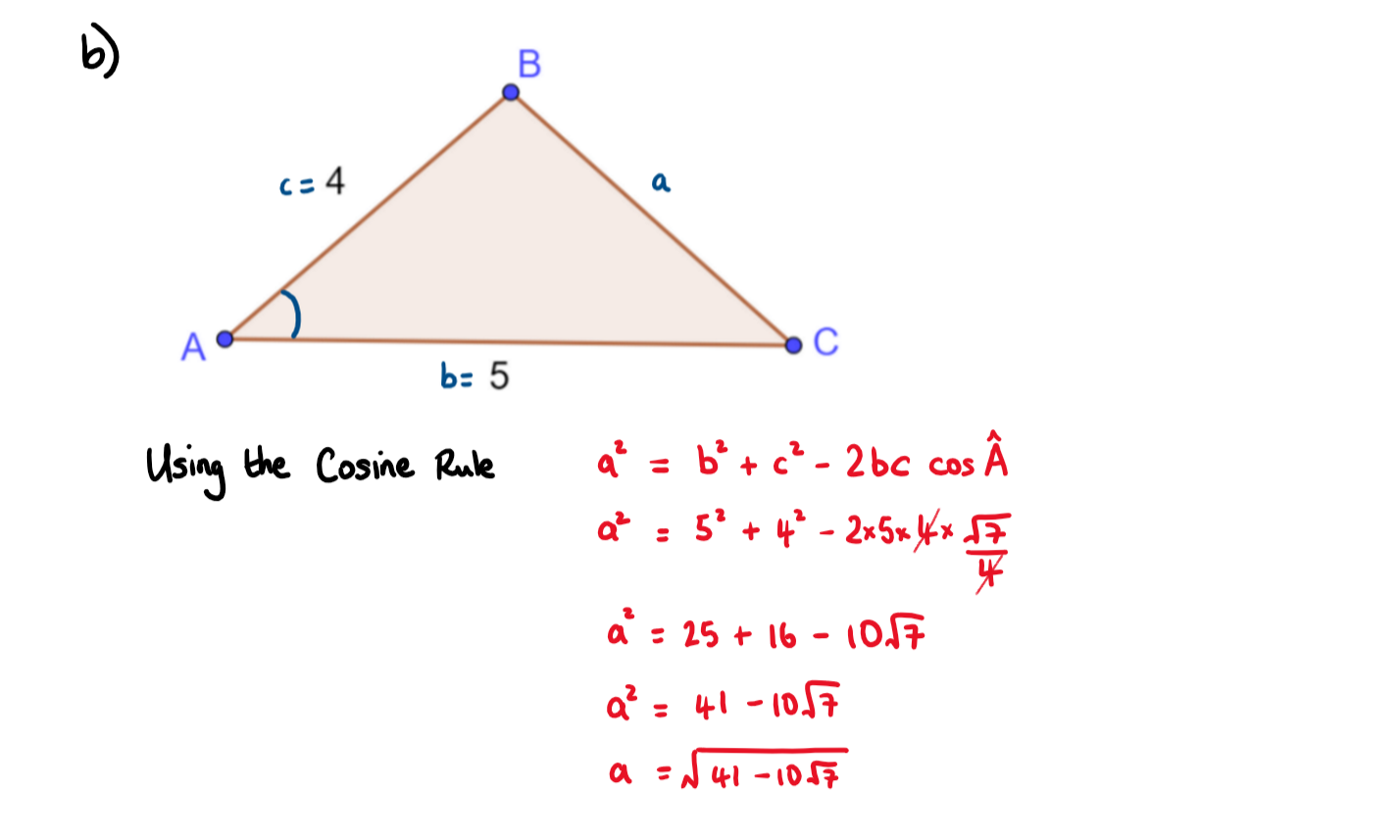
The following diagram shows triangle ABC with AB = 4 and AC = 5
 DIAGRAM NOT TO SCALE
DIAGRAM NOT TO SCALE
a) Given that \(\large \sin \hat A=\frac{3}{4}\), find the value of \(\large \cos \hat A\)
b) Hence, show that the length of \(\large BC=\sqrt{41-10\sqrt{7}}\)
Hint
a) You can use the Pythagorean identity \(\large \cos^2\theta+\sin^2\theta\equiv1\)
b) Use the Cosine Rule, c² = a² + b² - 2ab cosC
Full Solution



Prove that \(\large \frac{\sin ^3\theta}{\tan \theta}+\cos^3\theta\equiv\cos\theta\)
Hint
This is a very difficult proof for SL students!
There is always more than one way to carry out this proof.
Full Solution
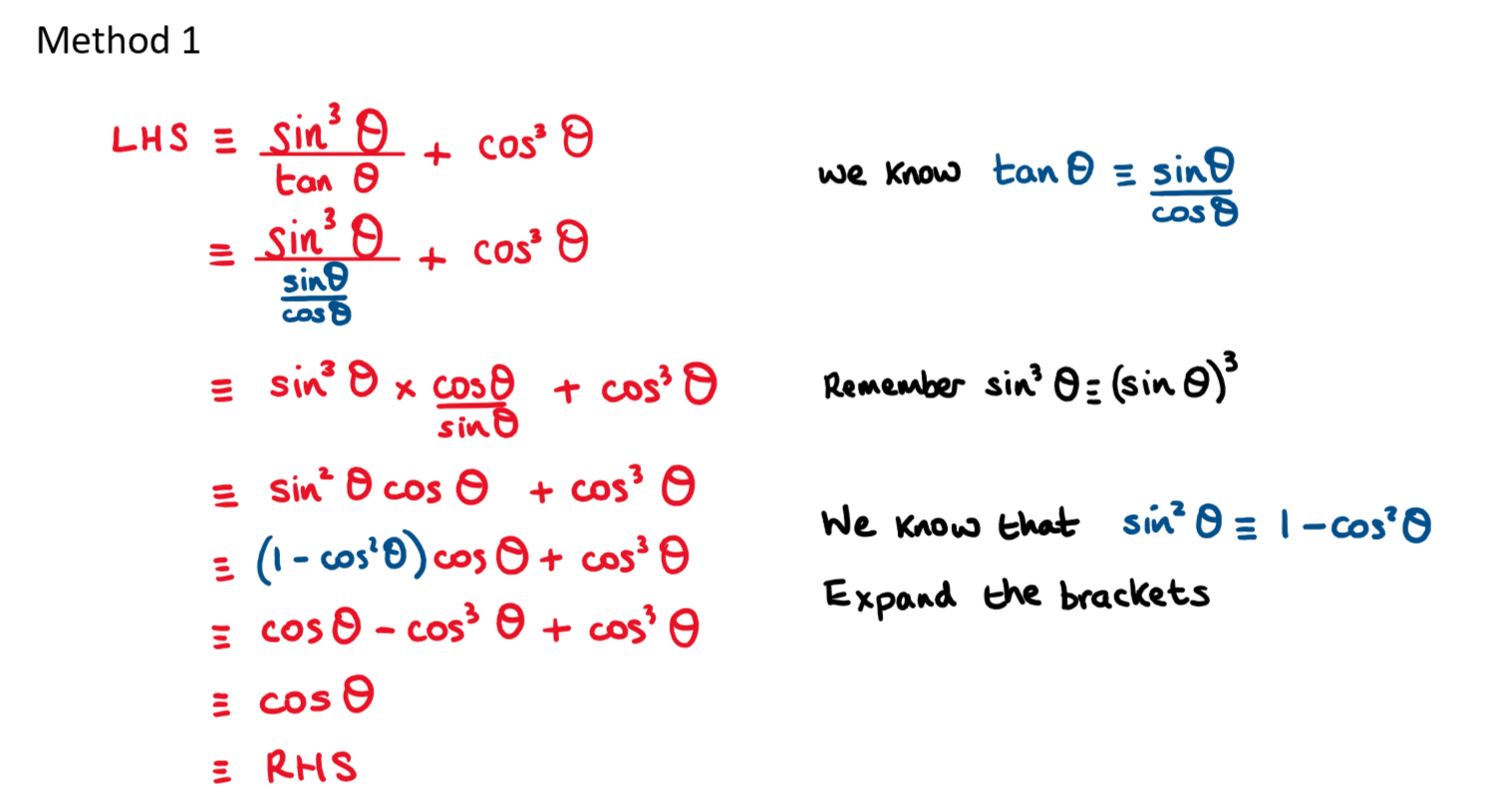
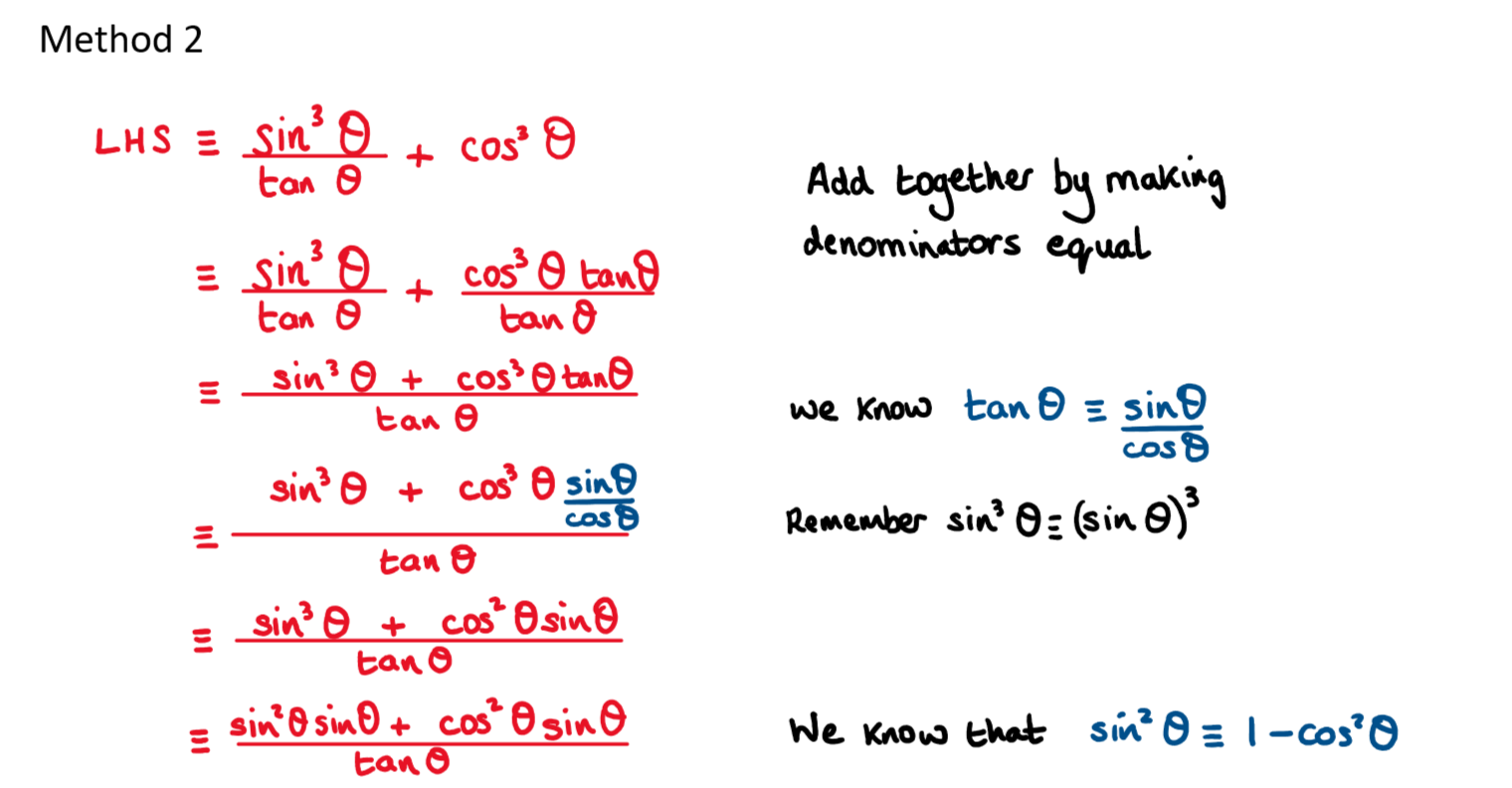



Let f(x) = (cos2x - sin2x)²
a) Show that f(x) can be expressed as 1 - sin4x
b) Let f(x) = 1 - sin4x. Sketch the graph of f for \(0\le x\le \pi \)
Hint
a) Expand the brackets
Consider the following identities \(cos^{ 2 }\theta +sin^{ 2 }\theta \equiv 1\\ sin2\theta \equiv 2sin\theta cos\theta \)
b) In order to sketch this function, consider the transformations from the graph of y = sinx
Full Solution
Print from here



Solve \(cos2θ=sinθ\) for \(0\le \theta \le 2\pi \)
Hint
Full Solution
Print from here



a) Show that \(cos2\theta-3cos\theta+2\equiv 2{ cos }^{ 2 }\theta -3cos\theta +1\)
b) Hence, solve \(cos2\theta-3cos\theta+2=0\) for \(0\le \theta \le 2\pi \)
Hint
Full Solution
Print from here



Let \(cos\theta=\frac{2}{3}\), where \(0\le \theta \le \frac { \pi }{ 2 } \)
Find the value of
a) \(sin\theta\)
b) \(sin2\theta\)
c) \(sin4\theta\)
Hint
a) Draw a triangle and work out \(sin\theta\)
c) Work out \(cos2\theta\) first. \(2\theta\) is obtuse
Full Solution
Print from here


Let f(x)= cosx and g(x) = \(\frac{2x^2}{1-x}\)
a) Show that g∘f(x) = 1 can be written as 2cos²x + cosx - 1 = 0
b) Hence solve g∘f(x)=1 for \(-\pi\le x\le \pi\)
Hint
a) Start by finding the compostive function g∘f(x).
b) This is a quadratic equation. Some students find it easier to factorise by substituting y = cosx and solving for y first.
Full Solution
Print from here


Solve \(\log _{ 3 }{ sinx-\log _{ 3 }{ cosx=0.5 } } \) for \(0\le x\le 2\pi\)
Hint
Use log laws to simlify equation: \(\log _{ a }{ \frac { x }{ y } =\log _{ a }{ x } -\log _{ b }{ y } } \)
Full Solution
Print from here


1 + cosx + cos²x + cos3x + ... = \(2 + \sqrt2\)
Find x given that \(-\frac {\pi}{2}\le x\le \frac {\pi}{2}\)
Hint
1 + cosx + cos²x + cos3x + ... is an infinite geometric series. Can you find the sum?
Full Solution
Print from here
How much of Geometry and Trigonometry Examination Questions SL have you understood?
Feedback
Which of the following best describes your feedback?


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn