5.4.4 Solving Problems Involving Magnetic Forces

Solving Problems Involving Magnetic Forces

There is a lot of mathematics surrounding magnetism and magnetic forces
The key equations are:

Force on a current-carrying conductor:
F = BIL

Force on a moving charge:
F = Bqv

Radius of a moving charge in a magnetic field:
r =

\frac{m v}{q B}

Below are two worked examples demonstrating different situations involving magnetic forces

Worked Example

A 5 cm length of wire is at 90° to the direction of an external magnetic field. When a current of 1.5 A flows through the wire it experiences a force of 0.06 N from the motor effect.

Calculate the magnetic flux density of the magnet.

Step 1: List the known quantities

Length, L = 5 cm = 0.05 m
Current, I = 1.5 A
Force, F = 0.06 N

Step 2: Write out the equation for magnetic force

F = BIL

Step 3: Rearrange the equation to make B the subject

B = \frac{F}{I L}

Step 4: Substitute values into the equation

$B = \frac{0.06}{1.5 \times 0.05} = 0.8 T$

Worked Example

This question is about the movement of an electrically charged particle into a magnetic field. An electron enters a magnetic field and moves in an approximately circular path as shown below.

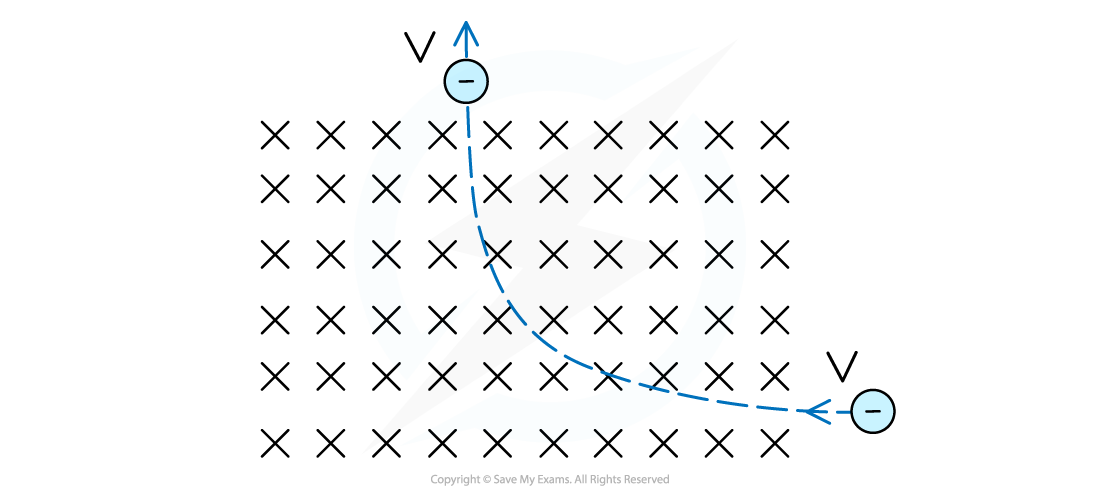
5-4-4-electron-movement-we2_sl-physics-rn

Explain whether the speed of the proton is the same when entering and exiting the magnetic field.
The magnetic field has a strength of 0.3 T and the velocity of the electron before entering the magnetic field is 8.6 × 10⁶ m s⁻¹ to the left. Show that the radius of the motion of the electrons is 1.63 cm.

Part (a)

- The answer is that the work done by the magnetic force on the charge must be zero
- This is because the force itself is at right angles to the velocity
- Since the work done is zero, therefore the kinetic energy does not change between entering and leaving the magnetic field
- Therefore the speed is the same

Part (b)

Step 1: List the known quantities

Magnetic field strength, B = 0.3 T
Velocity of electron (before entering field), v = 8.6 × 10⁶ m s⁻¹ to the left
Radius of motion to be shown, r = 1.63 cm

Step 2: Equate the magnetic force and the force of circular motion

This can be done for the situation since the circular motion is caused by the magnetic force

q v B = \frac{m v^{2}}{r}

Step 3: Rearrange the equation to find the radius

qvBr = mv²
qBr = mv

r = \frac{m v}{q B}

Step 4: Substitute in the values

r = \frac{(9.1 \times 10^{- 31}) \times (8.6 \times 10^{6})}{(1.6 \times 10^{- 19}) \times (3 \times 10^{- 3})} = 1.63 \times 10^{- 2} m

Step 5: State final answer

R = 1.63 × 10⁻² m = 1.63 cm in a circular motion

DP IB Physics: SL

Revision Notes

5.4.4 Solving Problems Involving Magnetic Forces

Solving Problems Involving Magnetic Forces

Worked Example

Worked Example

Author: Katie

Resources

Members

Company

Quick Links